Linear regression
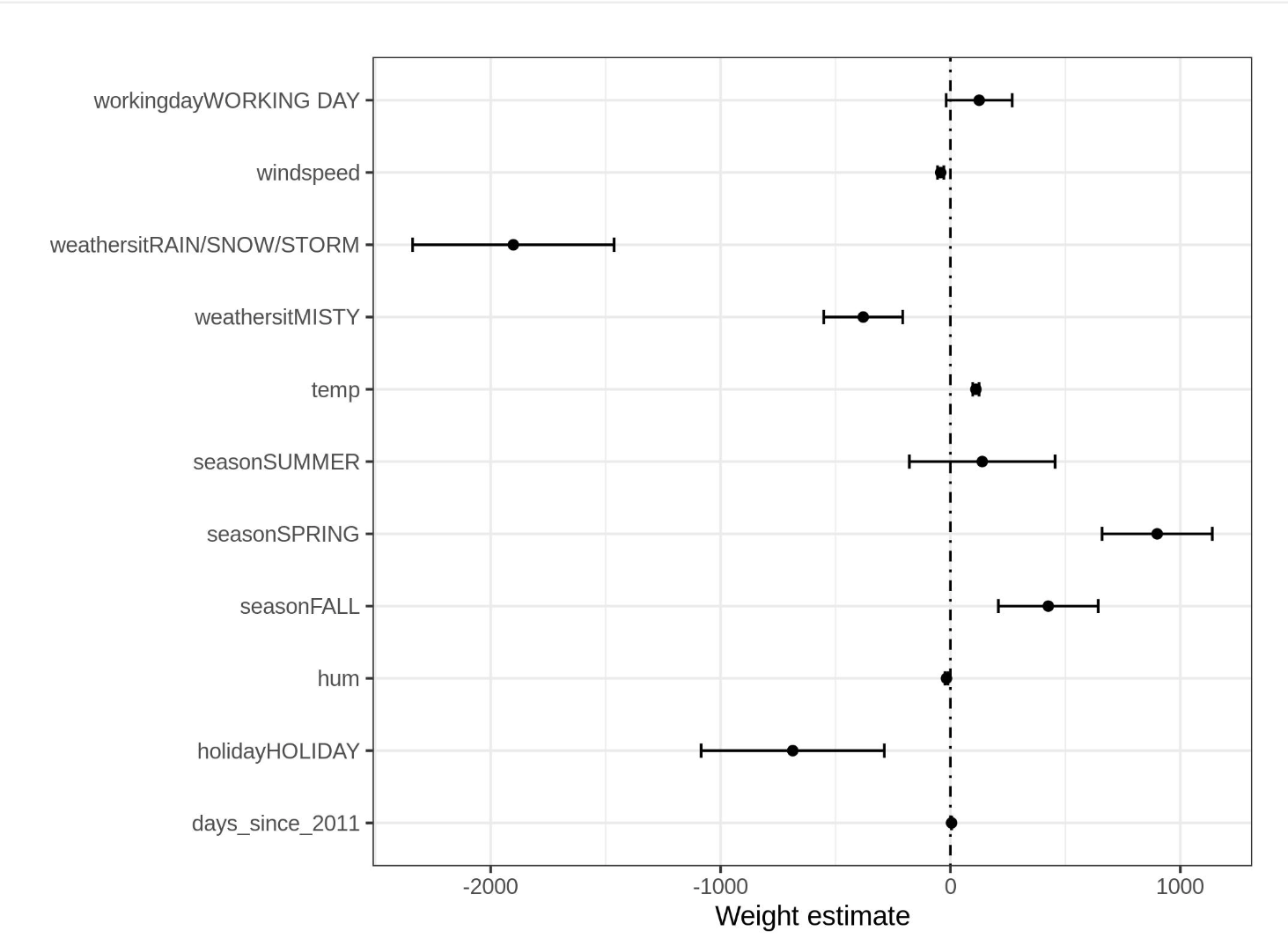
- Weights come with confidence intervals.
Assumptions of linear regression
- Linearity between independent and dependent features
- Target follows a normal distribution. If this assumption is violated, the estimated confidence interval of the feature weights are invalid
- Homoscedasticity (constant variance of errors for prediction) - Suppose the average error (difference between predicted and actual price) in your linear regression model is 50,000 Euros. If you assume homoscedasticity, you assume that the average error of 50,000 is the same for houses that cost 1 million and for houses that cost only 40,000. This is unreasonable because it would mean that we can expect negative house prices.
- Independence between data instances
- Fixed features - Features are free of measurement errors
- Absence of multicollinearity
Interpretation
- Increasing the numerical feature by one unit changes the estimated outcome by its weight
- Changing the categorical feature from reference category to the other category changes the estimated outcome by the feature’s weight
- For an instance with all numeric feature values at zero and categorical features at the reference categories, the model prediction is the intercept weight
- R-Squared increases with increase in number of features, even if they do not contain any information about the target value. We use adjusted R-Square, which accounts for the number of features used in a model.
- The importance of feature is measured by the value of t-statistic. The t-statistic is the estimated weight scaled with the standard error.
- Weight plot is used to visualize the weight and variance of the features
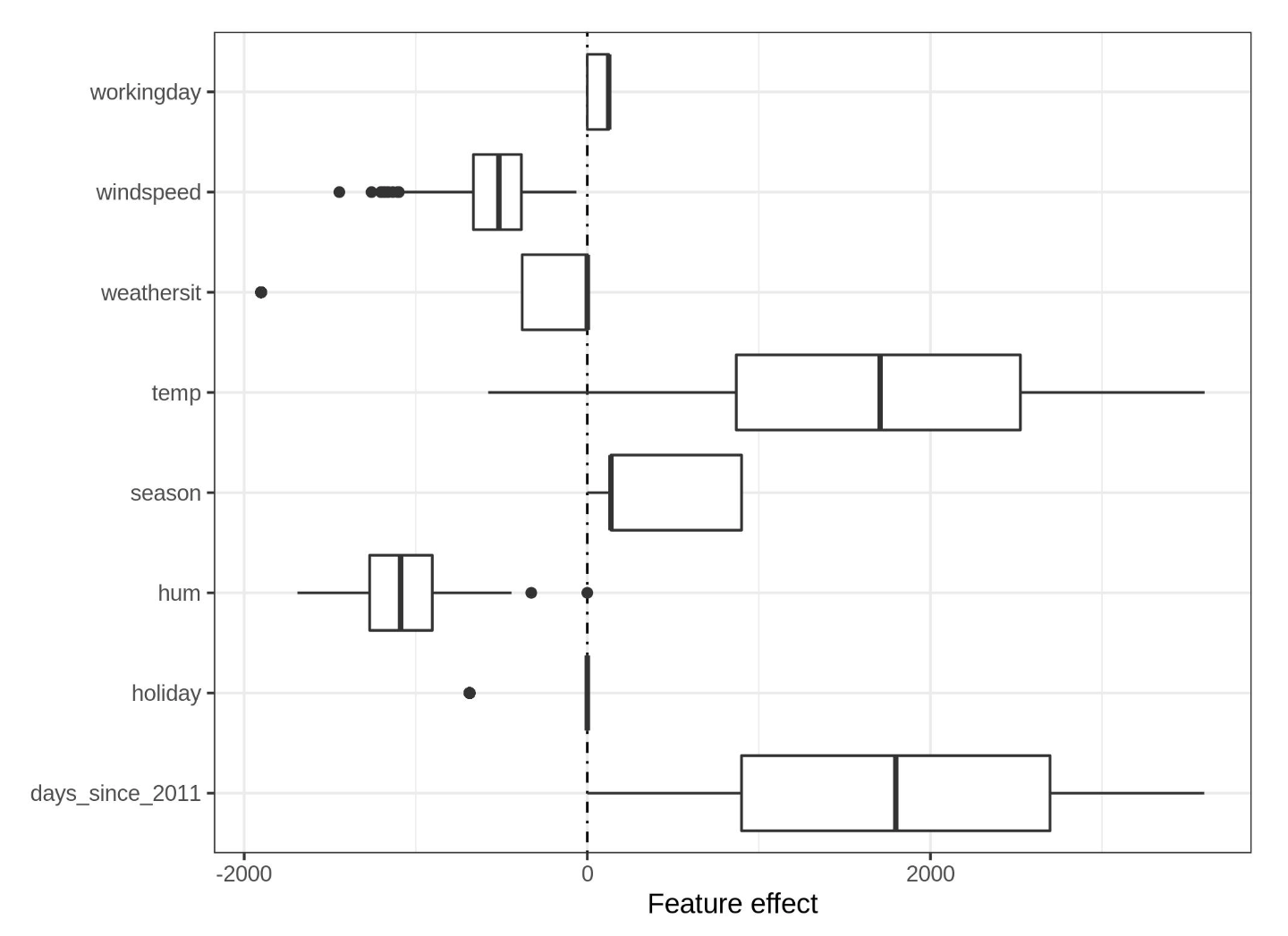
- Effect plot can help understand how much the combination of weight and feature contributes to the predictions in the data
 For individual prediction we can overlay the value for each feature on top of the effect plot
For individual prediction we can overlay the value for each feature on top of the effect plot 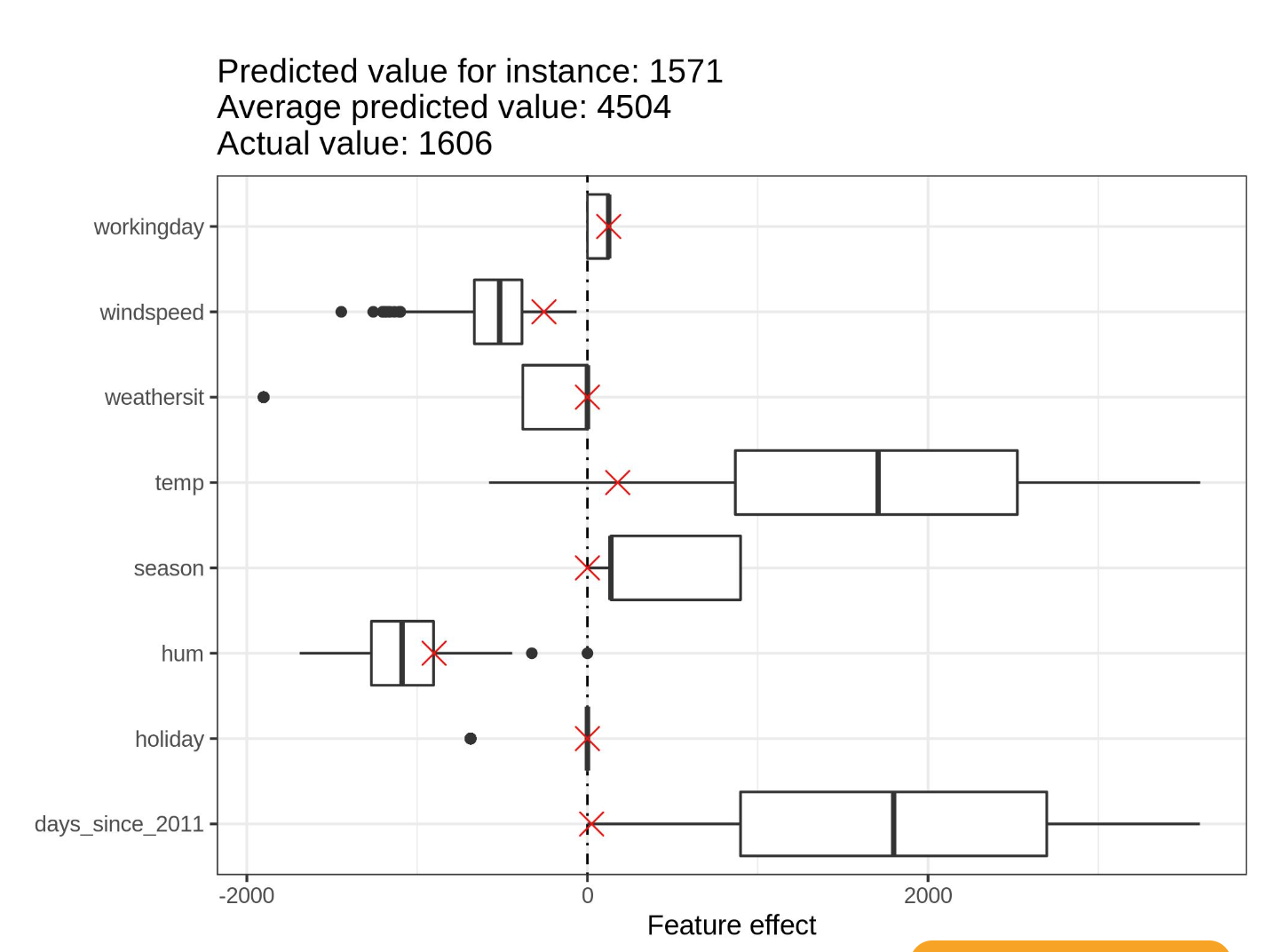
- In Lasso regression, we can use lambda as a parameter to control the interpretability of the model
Feature selection
- Forward selection: Fit a model with one feature. Do this for all the features. Select the model with high R-squared value. Keep adding features and selecting the best model. Continue till some criterion such as the max number of features are reached
- Backward selection: Similar to forward, here we keep removing features till some criterion is reached.
- Lasso can be used, as it considers all features simultaneously and can be automated.
Pros and Cons
Advantages
- Transparent model
- Comes with confidence intervals, tests etc
Disadvantages
- Non-linearities need to be hand-crafted
- Not good predictive performance
- The interpretation of weights can be unintuitive as it depends on all other features. House size and number of rooms are highly correlated. The weight of house size can be positive and number of rooms negative due to correlation.

 For individual prediction we can overlay the value for each feature on top of the effect plot
For individual prediction we can overlay the value for each feature on top of the effect plot 