Eigenvalues and Eigenvectors

Bases

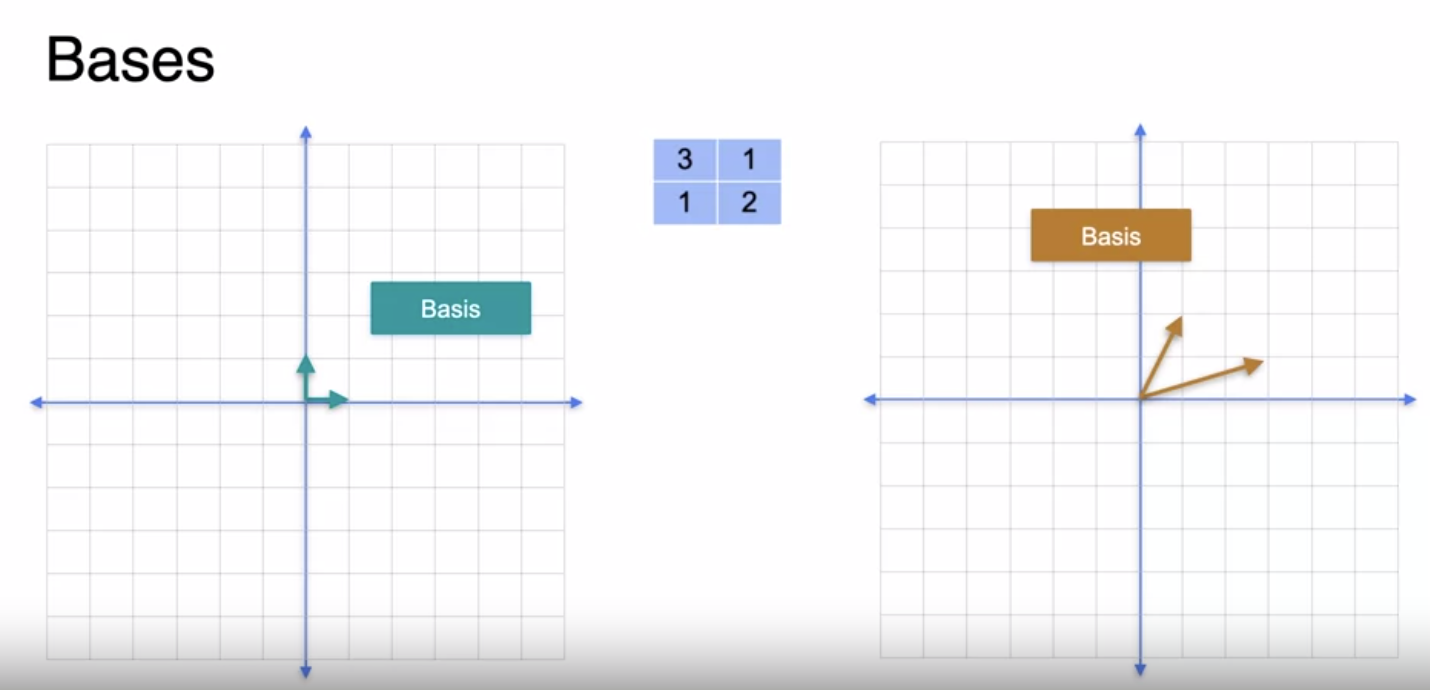
  • Basis

  • The main property of a Basis is that every point in the space can be expressed as a linear combination of elements in the basis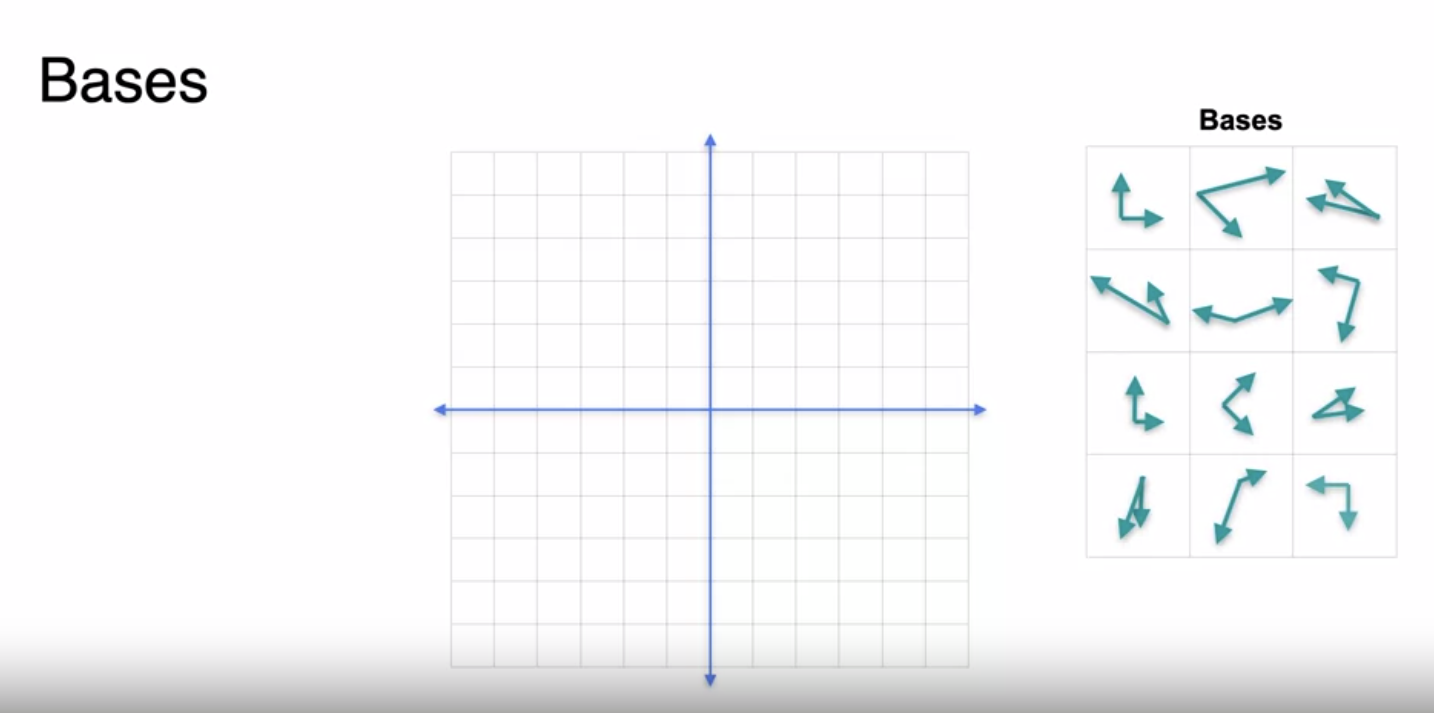

  • Valid Basis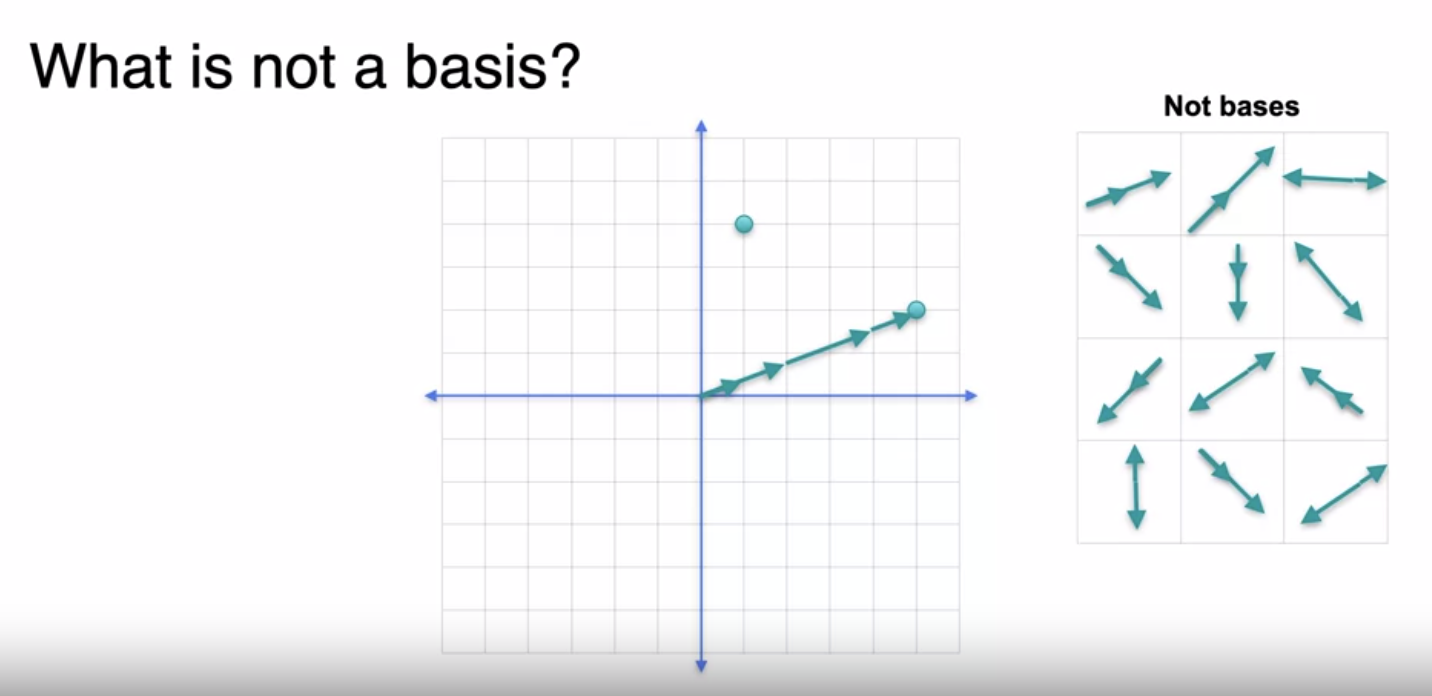

  • Invalid Basis

Span

  • The span of a set of vectors is simply the set of points that can be reached by walking in the direction of these vectors in any combination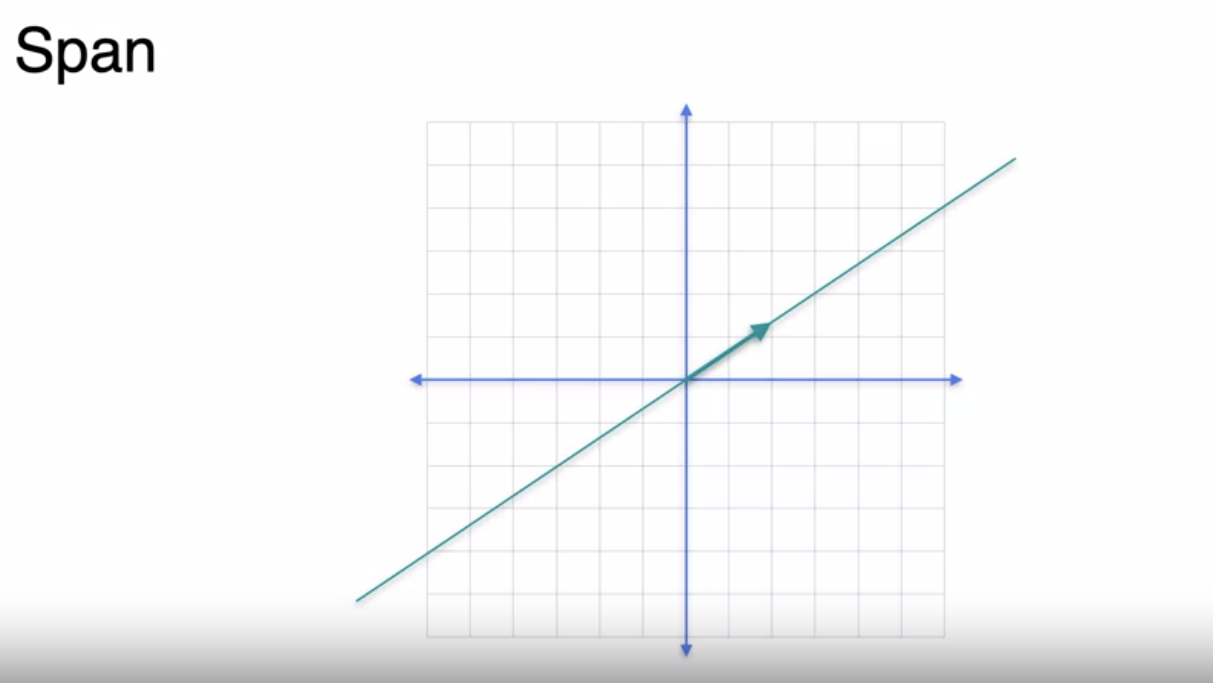

  • Span of a vector

  • A basis is a minimal spanning set

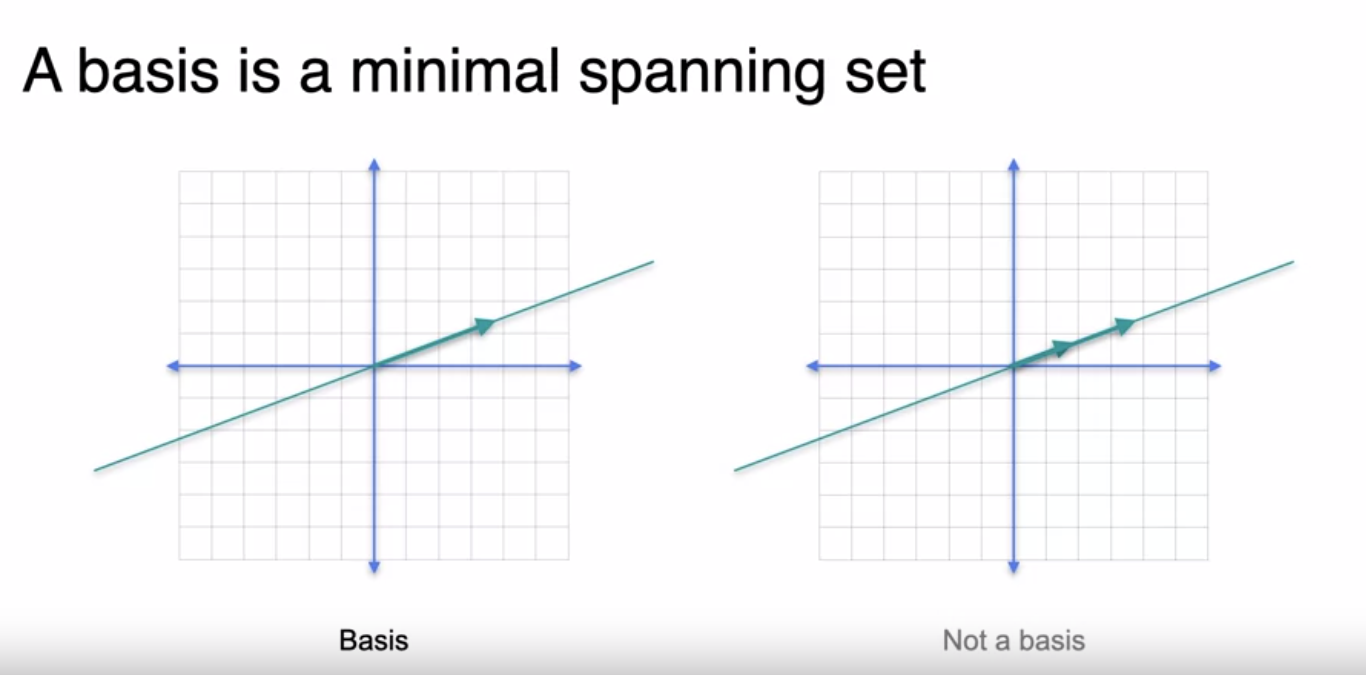
  • Minimal Spanning Set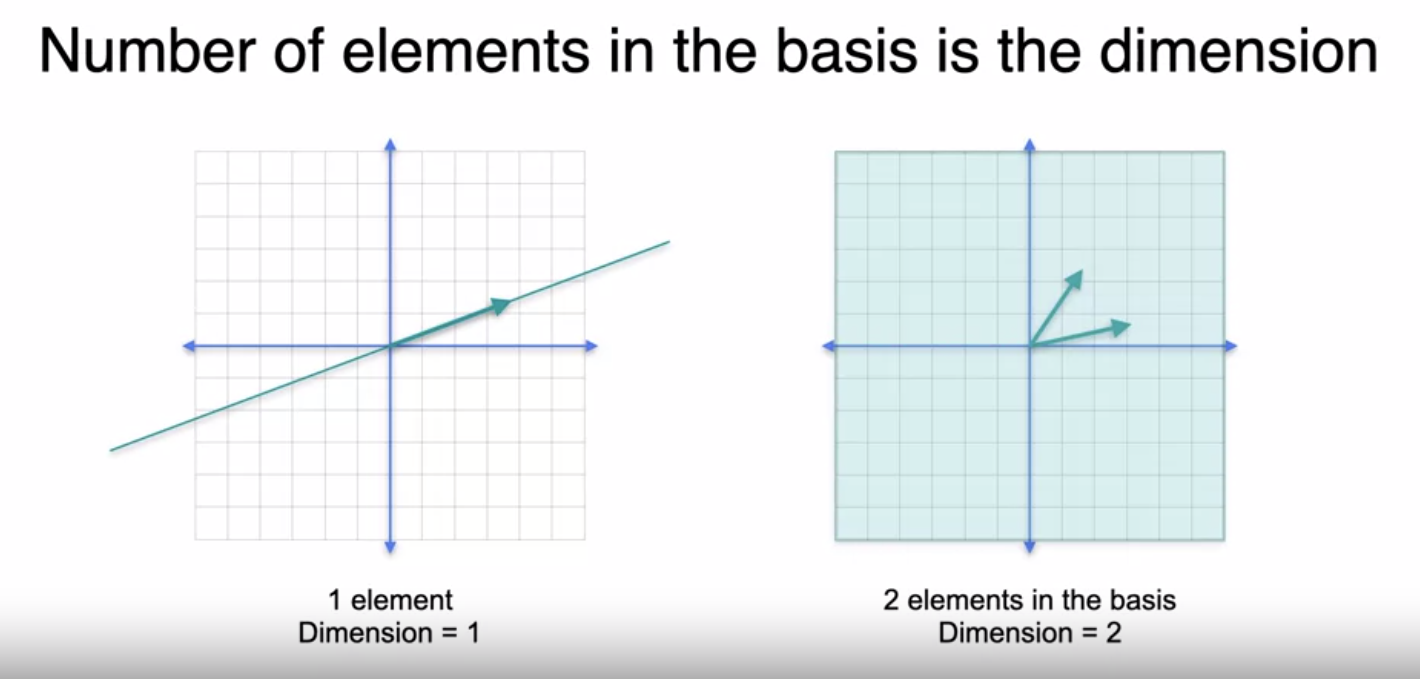

  • Number of elements in the basis is the dimension

    Eigenbases

    • Some basis are more useful than others

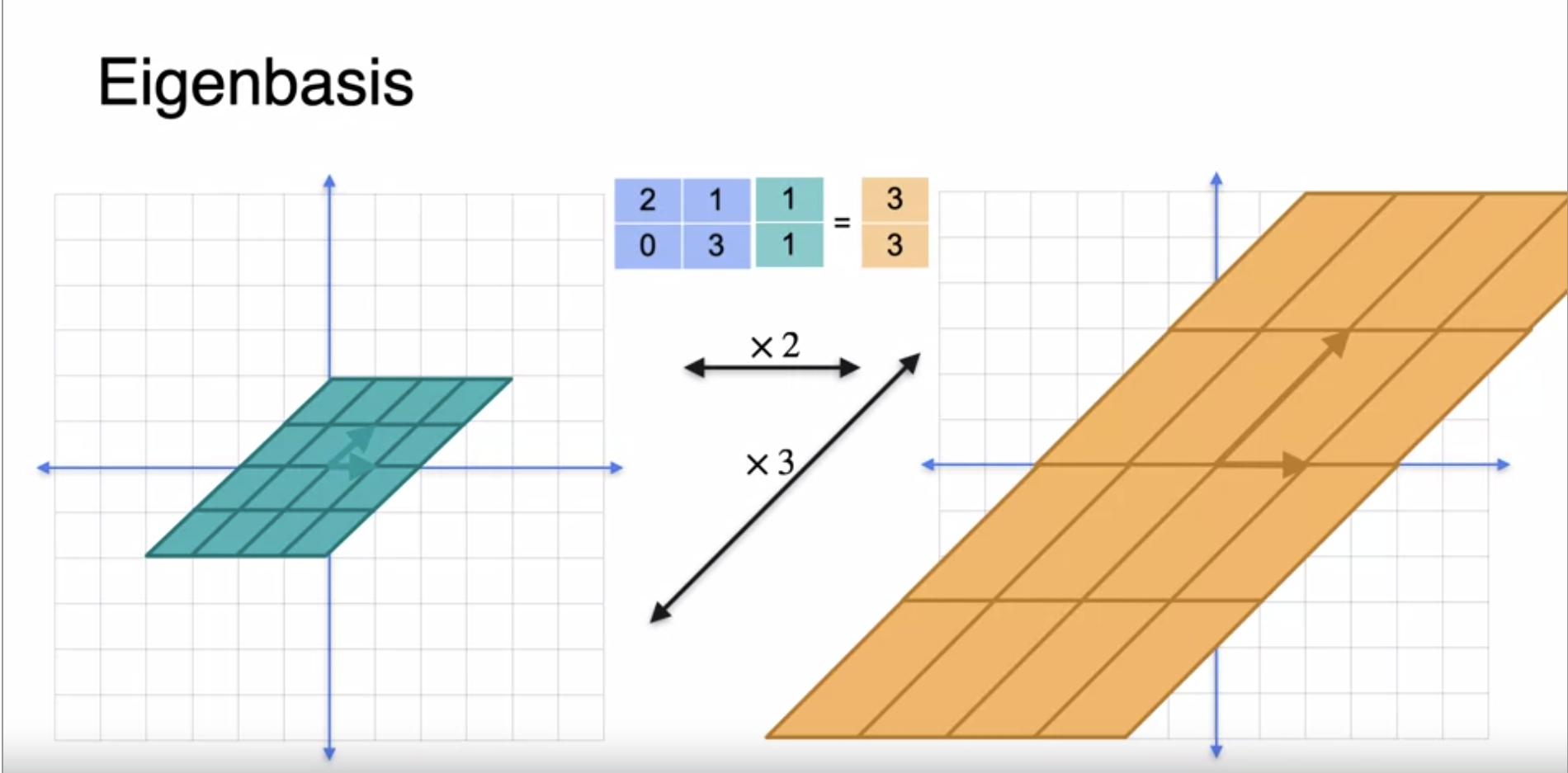
    • Eigenbases

    • Eigenbases - A special way of linear transformation with respect to a basis that sends a parallelogram to another parallelogram with sides parallel to the original one. The basis is streched in the two directions (in the below case) which is called eigenbasis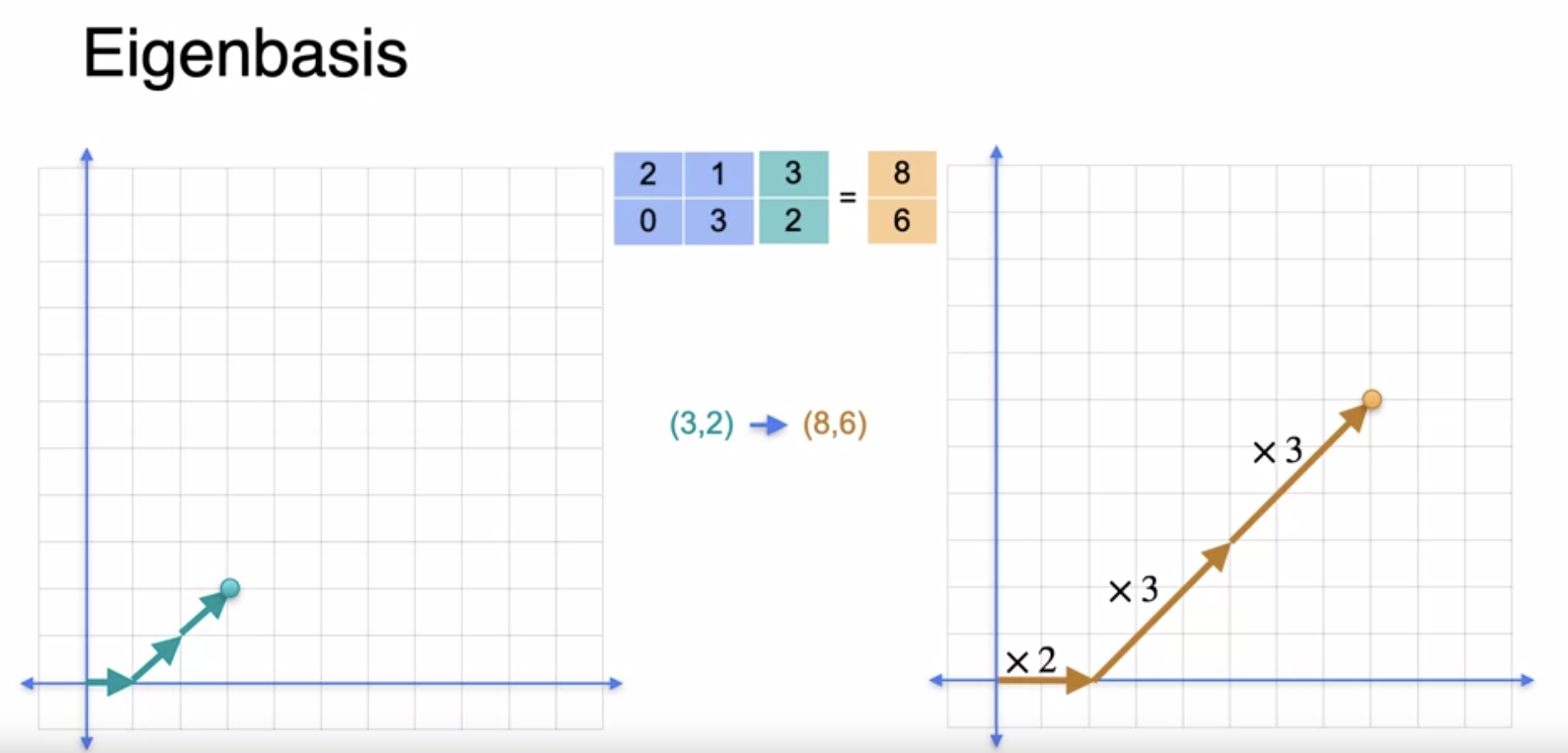

    • Eigenvectors and Eigenvalues

    • In the linear transformation, the two vectors in the basis are called Eigenvectors and the streching factor are called Eigenvalues

Eigenvalues and Eigenvectors

Finding Eigenvalues

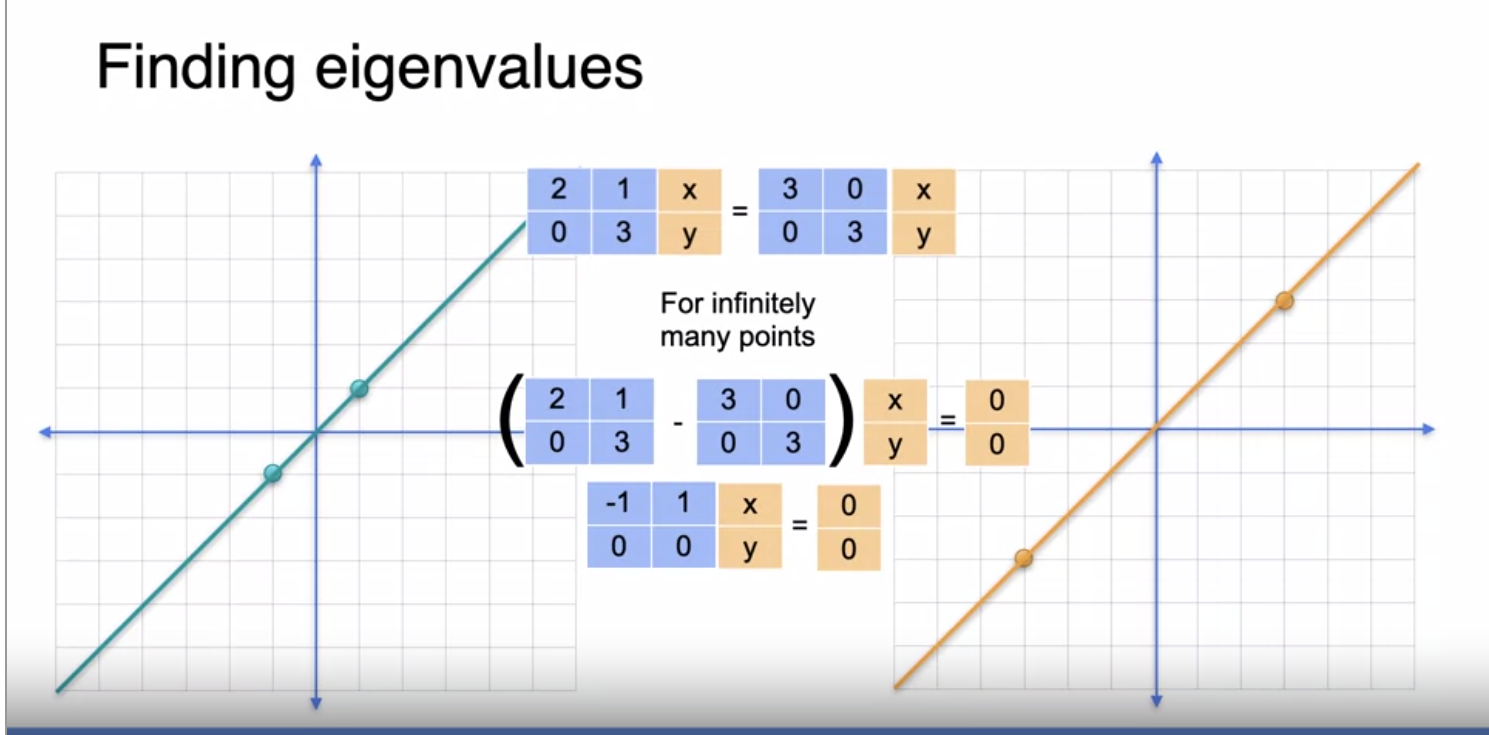
  • Finding Eigenvalues

  • Finding Eigenvalues using characteristic polynomial

Finding Eigenvectors

  • Finding Eigenvectors using Eigenvalues

Resources to learn more

Reference