Probability
probability = preferred events / All events
Union is similar to ‘OR’ condition
Intersection is similar to ‘AND’ condition
Probability of getting event A or B is
- P(A U B) = P(A) + P(B) - P(A and B)
- We are subtracting P (A and B) because some elements will be common to both A and B and we will be double counting them. So we subtract P (A and B) to eleminate the double count
- P(A U B) = P(A) + P(B) - P(A and B)
We can use Venn diagram to draw intersections, mutually exclusive probabilities etc. Venn diagrams can’t be used for conditional probabillity or to show dependence
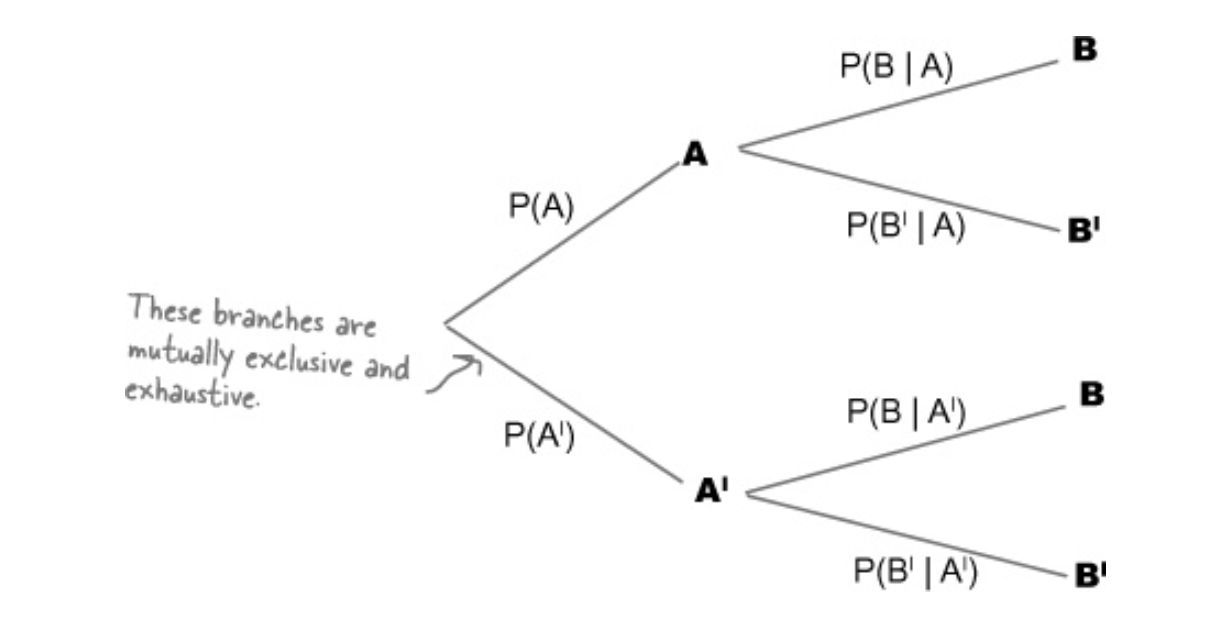
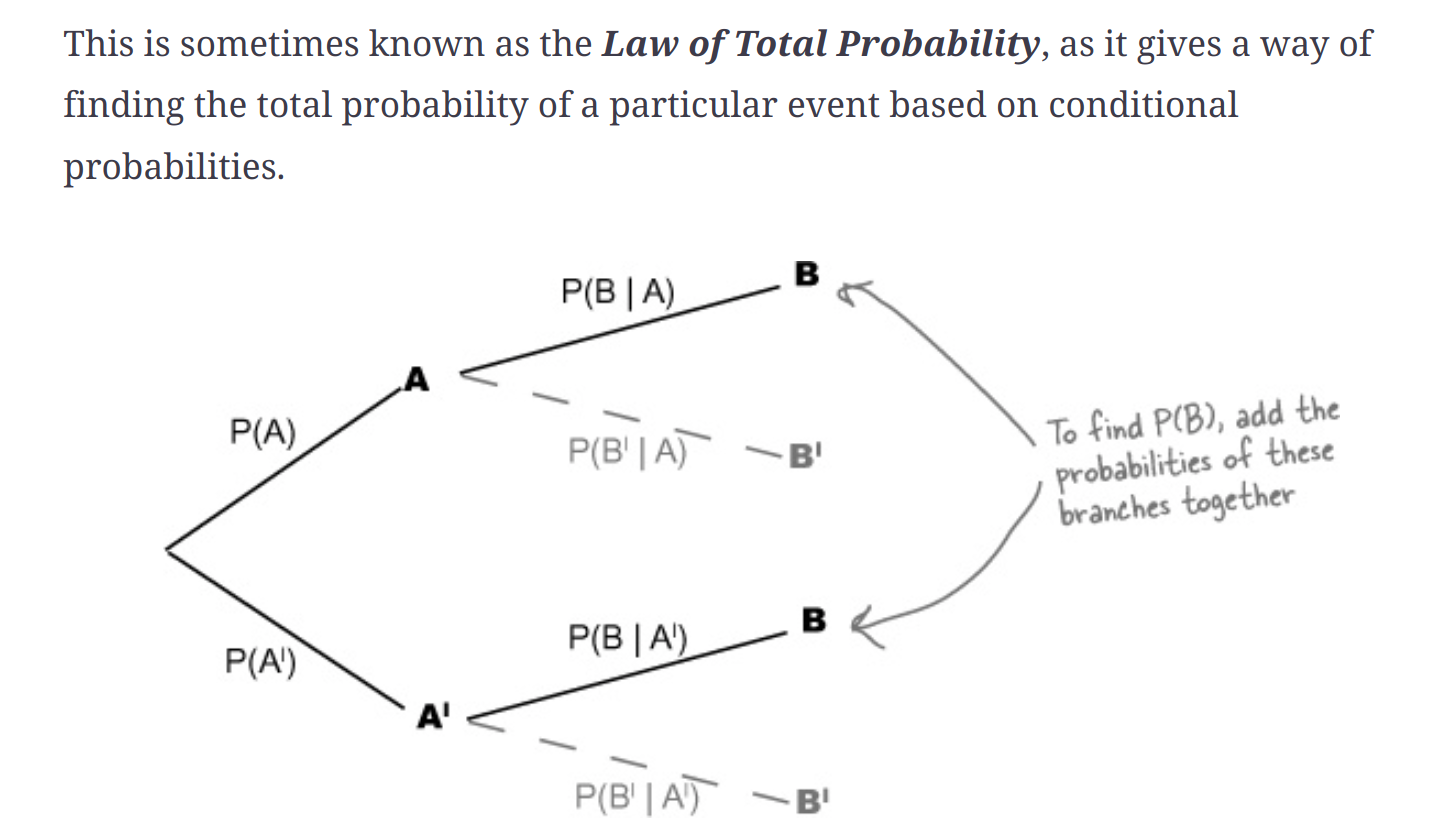
We can use tree diagrams to visualize conditional probability and dependence
Probability of A given B - P(A | B)

If two probabilities are independent then:
- P(A|B) = P(A) because A and B are independent and A does not depend on occurance of B, we can use this expression to check if two events are independent
- P( A and B) = P(A|B)* P(B) as P(A|B) = P(A)
- P(A and B) = P(A) * P(B) - when two events are independent then we need to multiply their probabilities
- If two probabilities are independent then they are not mutually exclusive. If probabilities are mutually exclusive then they are not independent
Mutually exclusive events - Add the probabilities - P(A U B) = P(A) + P(B) because P(A and B) will be zero
Bayes Thereom
- When we are provided information about a conditional probability eg P(A|B) and if we need to find the conditional probability P(B|A) then we should use Bayes theorem