Linear Transformations

Matrix - Vector multiplication as a Linear Transformations

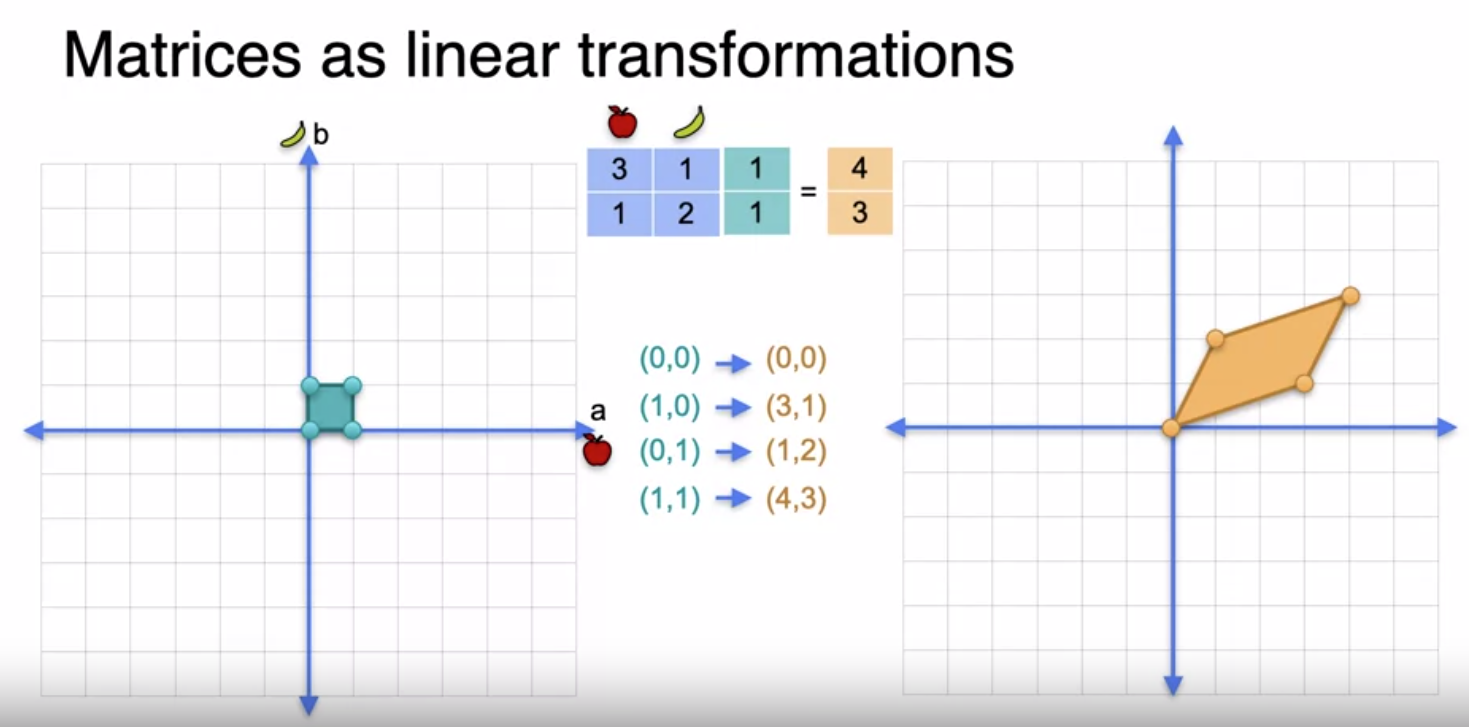Matrices as a Linear Transformations Basis cover the entire plane * Matrix vector multiplication as a linear transformation * To get the matrix from original and transformed vectors, we only need information for two vectors [0,1] and [1,0] (see the image below) * Getting the matrix back from the original and transformed vectors

Matrix Multiplication

  • We can see matrix product as multiplying two matrix and also as combining two linear transformations into a third linear transformation

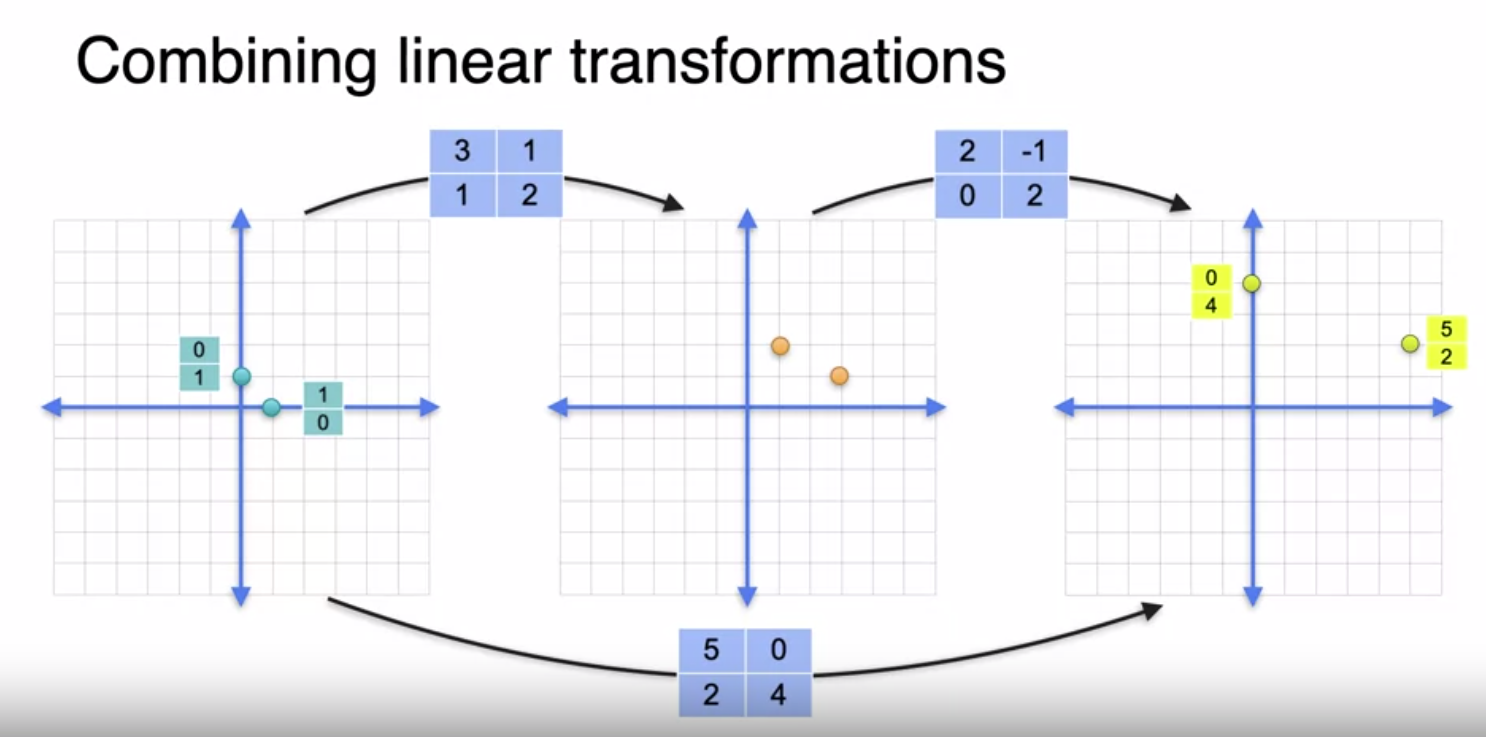
  • Matrix multiplication as combining linear transformations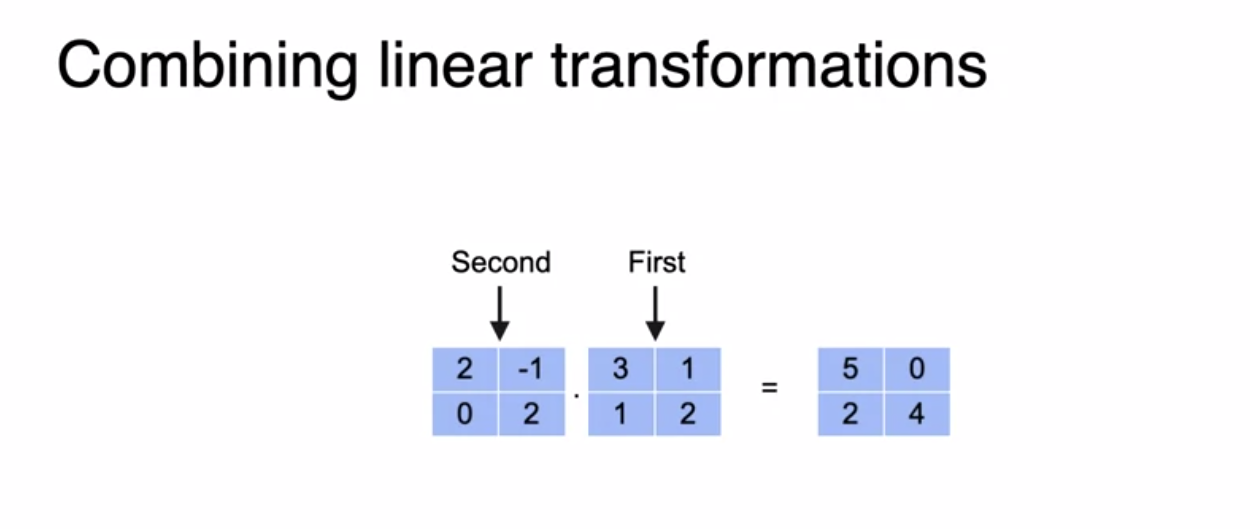

  • Matrices flipped

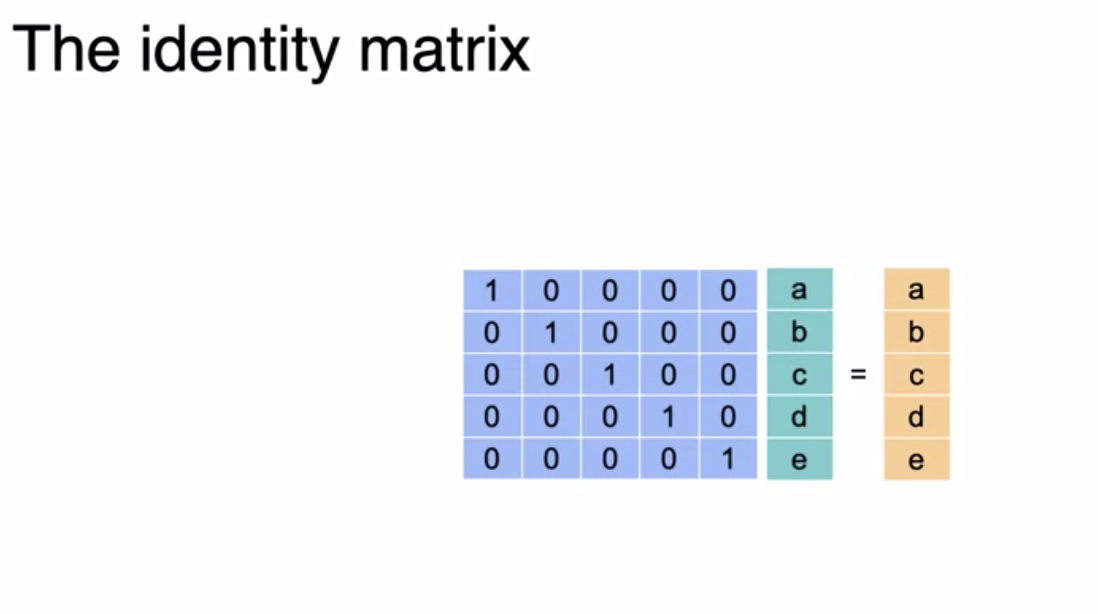
Indentiy Matrix

  • It is the matrix when multiplied by any other matrix will give the same matrix
  • Linear transformation by an Identity Matrix will leave the plane intact
  • Identity Matrix

Matrix Inverse

  • The product of a matrix and its Inverse should be an Identity matrix

  • Inverse Matrix reverses the linear transformation of a matrix

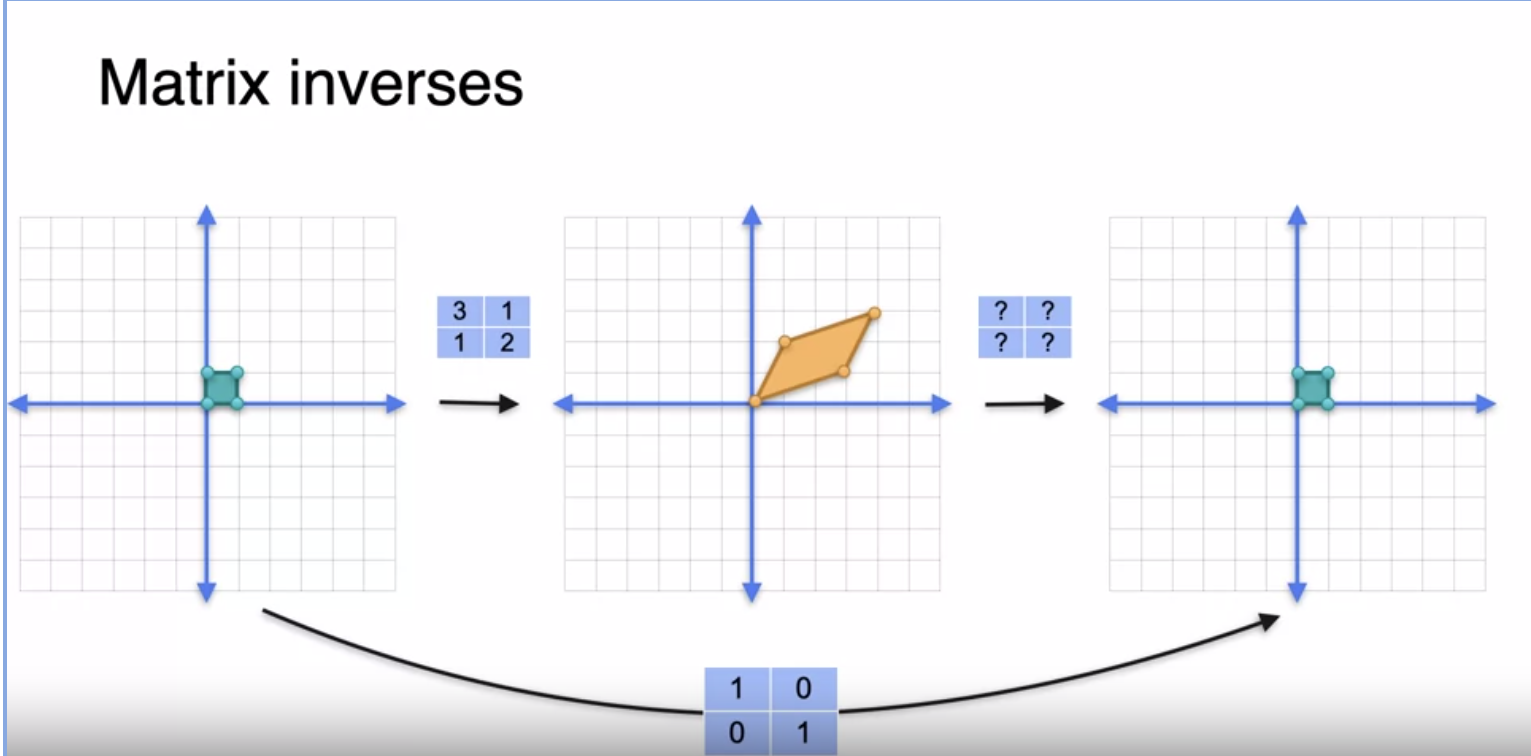
  • Matrix Inverse

  • Finding Matrix Inverse

  • Non-singular matrices will have inverse and singular matrix will not have inverse

  • Matrix with determinant zero will not have inverse