Solving linear Equations
Matrix row-reduction
To solve linear equation using traditional method, we use elimination. Similarly we use row reduction when using matrices to solve linear equations

Matrix row-reduction 
Row echelon form for singular matrix
Row operations
- Row operations preserve the singularity of the matrix i.e singular matrix will be singular and non-singular matrix will be non-singular after row operations
- row operations are -
- switching rows
- Multiplying a row by a non-zero scalar
- Adding a row to another row
The Rank of a Matrix
It is a measure of the information that matrix or its corresponding system of linear equations is carrying
Matrices with reduced rank will take less space for storage

Matrices with reduced rank to compress the images 
Rank fo a matrix There is a relationship between Rank of a Matrix and its solution space.
Rank = number of rows in a matrix - Dimension of solution space
A matrix is non-singular if and only if it has full rank. The number of rows is equal to the rank of the matrix
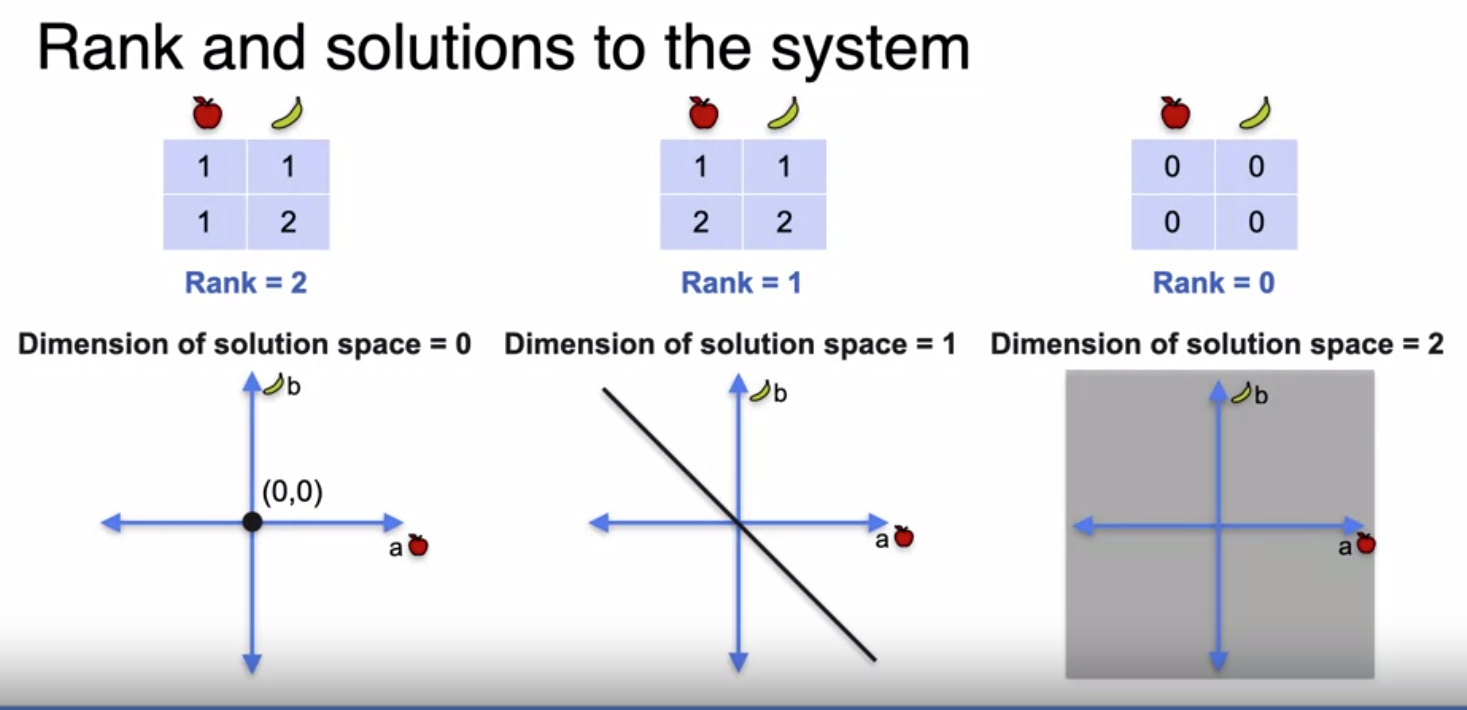
Rank and Solution space of a Matrix 
Rank of matrices
Row Echelon Form of a Matrix
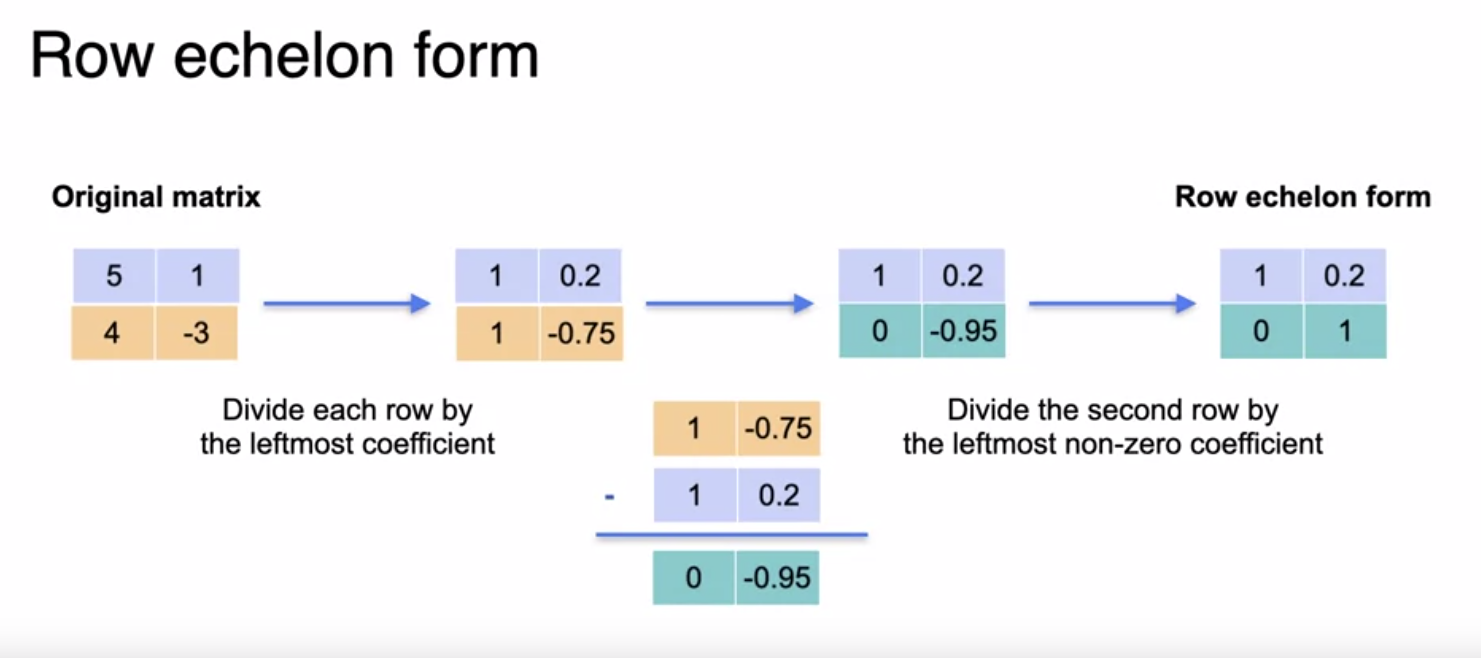
Calculations to get Row Echelon Form Rank of a matrix is the number of 1’s in the diagonal of row echelon form (for the below figure)

Relation between Row Echelon form, Singularity and Rank 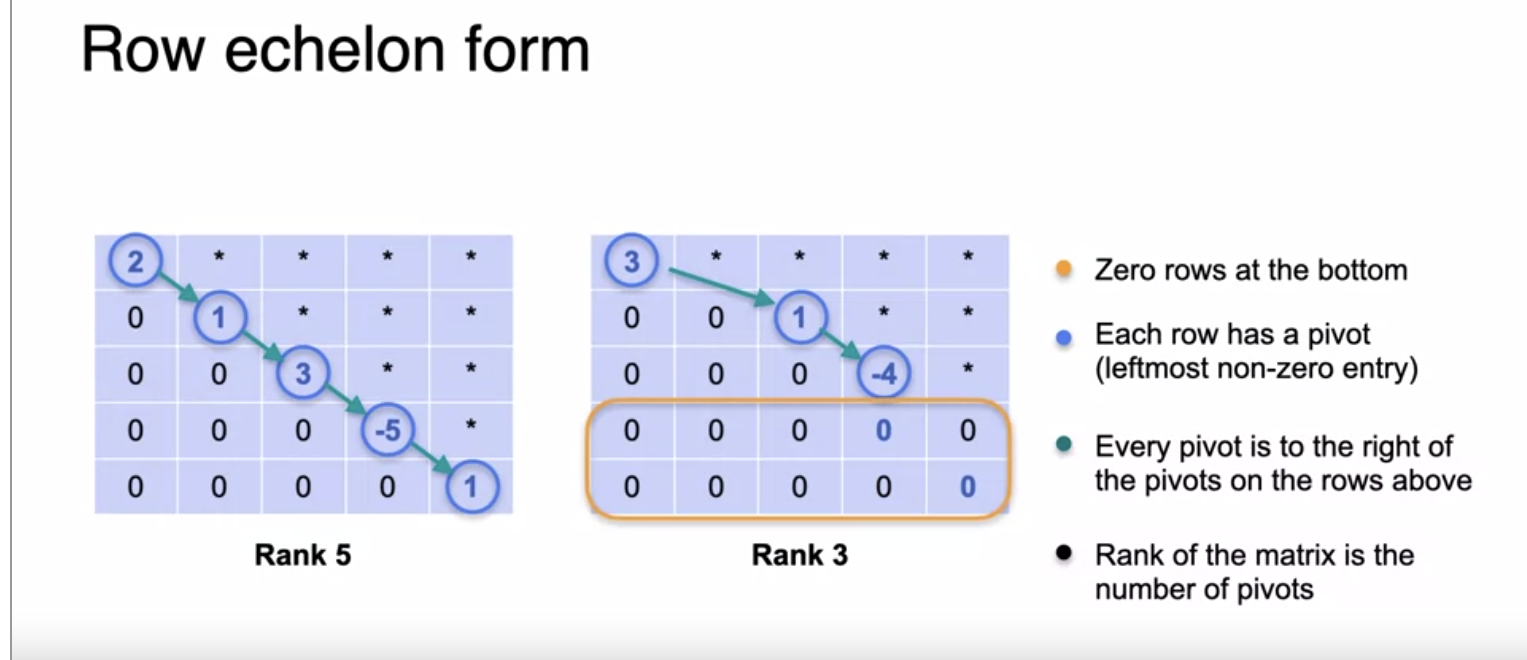
Row Echelon for Bigger Matrices
Reduced Row Echelon Form
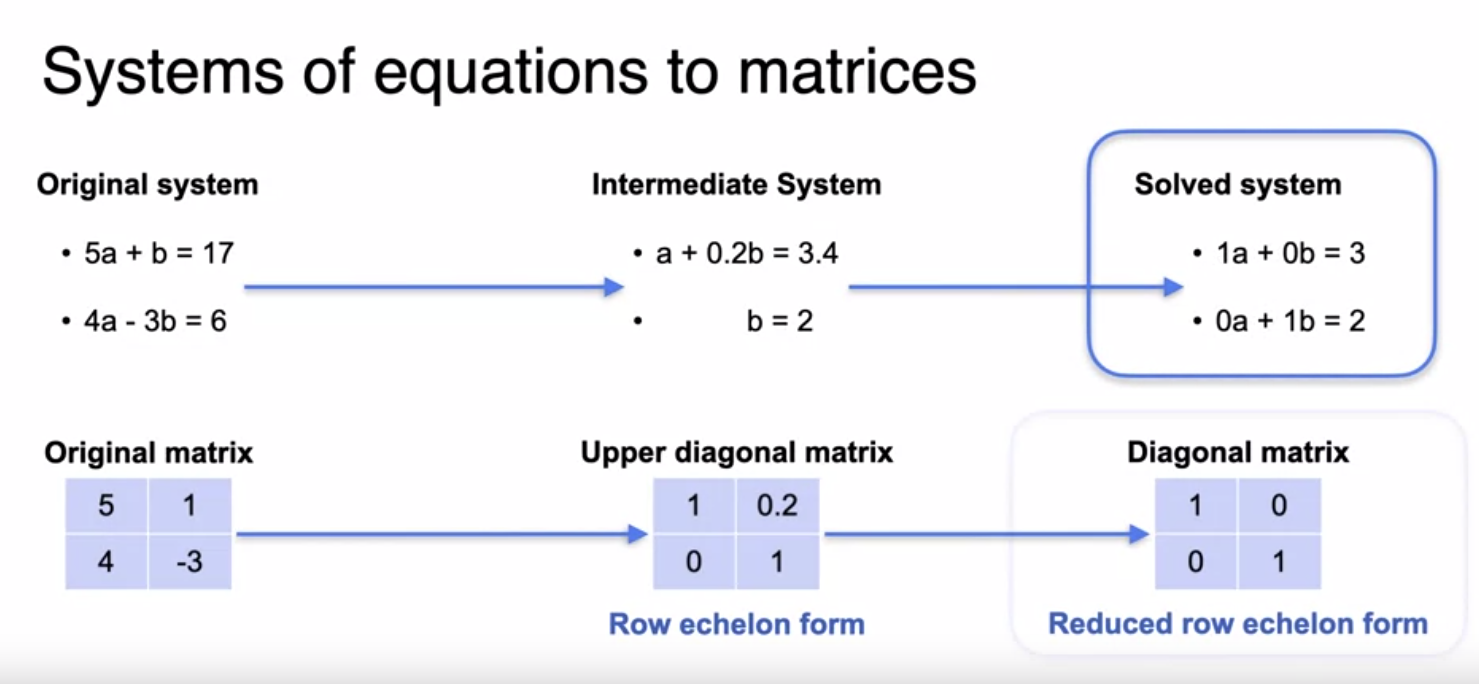
Reduced row echelon form is equivalent to the solved system 
Generalized form of Reduced row echelon 
Calculating Reduced row echelon