XGBoost
Newton Boosting combines advantages of Adaboost and Gradient Boosting. It uses weighted gradients (weighted residuals) to identify the most misclassified examples.
Gradient Descent is first order derivative. Newton's method or Newton Descent is a second order optimization method. It uses both first and second order derivative information during optimization.
Newton’s method for Minimization
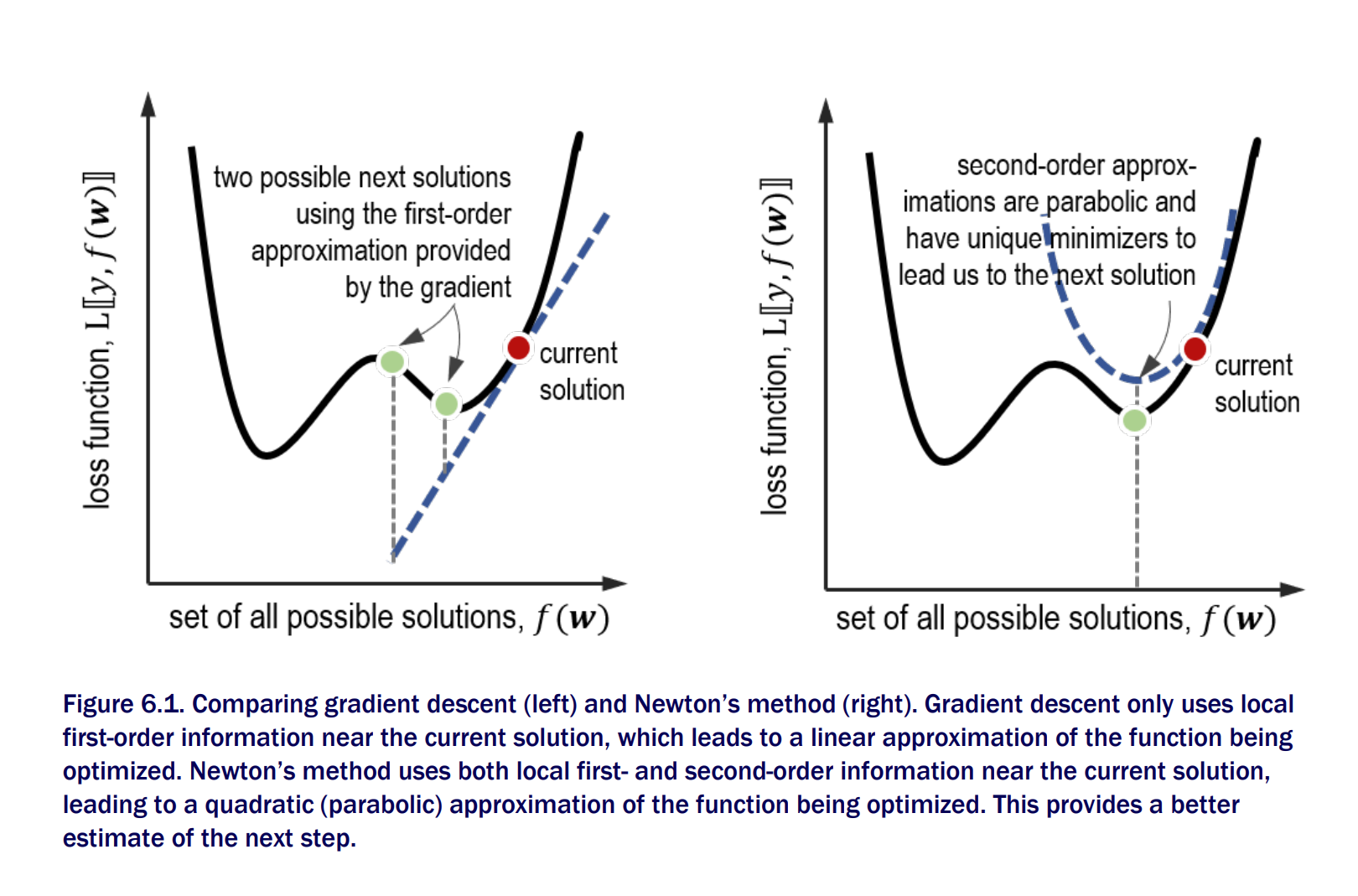
Newton’s Method vs gradient descent 
Taking second derivative 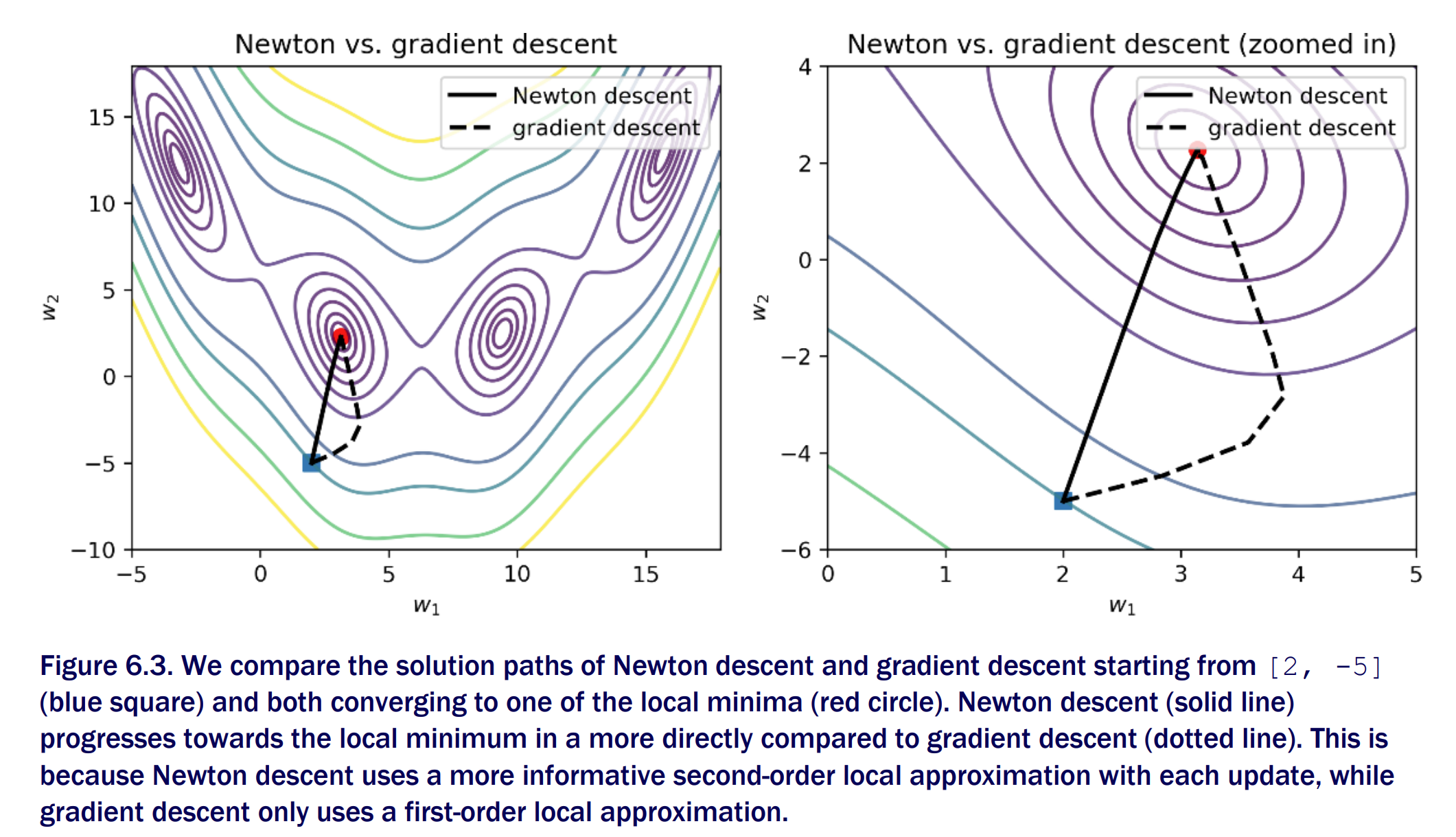
Newton’s Method vs gradient descent
Properties of Newton Descent
- It computes the descent step exactly and does not require a step length
- It is sensitive to our choice of initial point. Different initializations will lead Newton descent to different local minimizers.
- It is a powerful optimization method. It converges to solutions much faster as it takes local second-order derivative information (essentially curvature) into account in constructing descent directions. This comes at a computational cost. With more variables, the second derivative or Hessian becomes difficult to manage, especially as it has to be inverted.
Newton Boosting: Newton’s Method + Boosting
AdaBoost identifies and characterizes misclassified examples that need attention by assigning weights to them: badly misclassified examples are assigned higher weights. A weak classifier trained on such weighted examples will focus on them more during learning. Gradient boosting characterizes misclassified examples that need attention through residuals. A residual is simply another means to measure the extent of misclassification and is computed as the gradient of the loss function.
Newton boosting
does both and uses weighted residuals. The residuals in Newton boosting are caclulated using the gradient of the loss function (the first derivative). The weights are computed using the Hessian of the loss function (the second derivative)Newton boosting avoids the expense of computing the gradient or the Hessian by learning a weak estimator over the individual gradients and Hessians
Newton boosting uses Hessian-weighted residuals, while gradient boosting uses unweighted residuals
what does Newton Boosting do?

Newton Boosting for a single example Hessians incorporate local curvature information to ensure that training examples that are badly misclassified get higher weights
XGBoost: A framework for Newton Boosting
- Distributed and parallel processing capabilities
- Newton boosting on regularized loss functions to directly control the complexity of weak learners
- Alogrithmic speedups such as weighted quantile sketch for faster training
- Block based system design that stores data in memory in smaller units called blocks. This allows for parallel learning, better caching, efficient multi-threading
- Support for a lot of loss functions
Regularized loss functions
- XGBoost uses tree based methods to control the complexity of the model.
- Instead of using Gini or Entropy XGBoost uses regularized learning objective
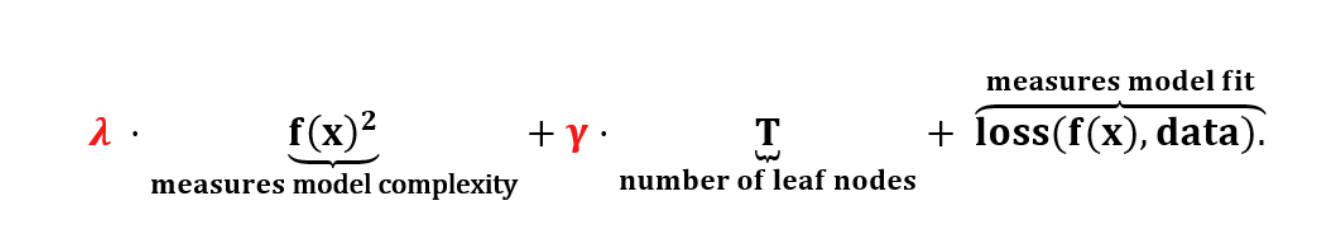
Quantile based Newton Boosting
- Find ideal split points using qunatiles in the features
- Instead of using evenly sized bins, XGBoost bins data into feature-dependent buckets.
Imp points
- In boosting algorithms we select the learning rate to help us avoid overfitting (instead of convergence)