T-SNE (T distributed - Stochastic Neighbour Embedding)

  • Neighbour Embeddings - Preserve the nearest neighbours instead of preserving distances

Stochastic Neighbour Embedding

  • Loss function is KL divergence between pairwise similarities in the high-dimensional and in the low-dimensional spaces. Similarities are defined such that they sum to 1
  • High price for putting close neighbors in high dimensions far away
  • If the distance between points high then their similarity is less and vice versa
  • SNE Formula

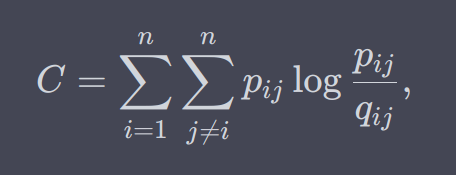
Chatgpt explanation of SNE formula

  • Formula Explanation by Chatgpt

Calculating High-dimensional Similarity

  • High-dimensional Similarity
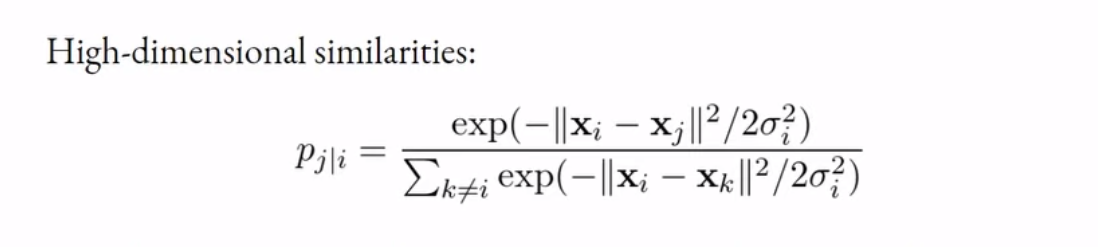
  • Kernel width by default is chosen such that 30 values are large and others should be zero (perplexity - 30)

Calculating low-dimensional Similarity

  • Low-dimensional Similarity

Optimization

  • we can use Gradient Descent for optimizing the loss
  • This works as a many body simulation: close neighbors attract each other while all points repulse each other
  • Gradient Descent

Early exaggeration

  • During the early stages of iteration to keep the similar points together, the attractive forces between nearby points are amplified, making them more dominant than the repulsive forces between distant points. (if this is not done, then it was observed that the quality of the output is not good)
  • After a few steps, early exaggeration is turned off, then repulsion will expand the clusters

Speeding up T-SNE

  • Vanilla T-SNE is quadratic complexity
  • To speed up we need to take care of Attractive and repulsive forces

Attractive Forces

  • Use a small number of non-zero affinities i.e. sparse k-nearest neighbour (KNN) graph.
  • Using approximate KNN

Repulsive forces

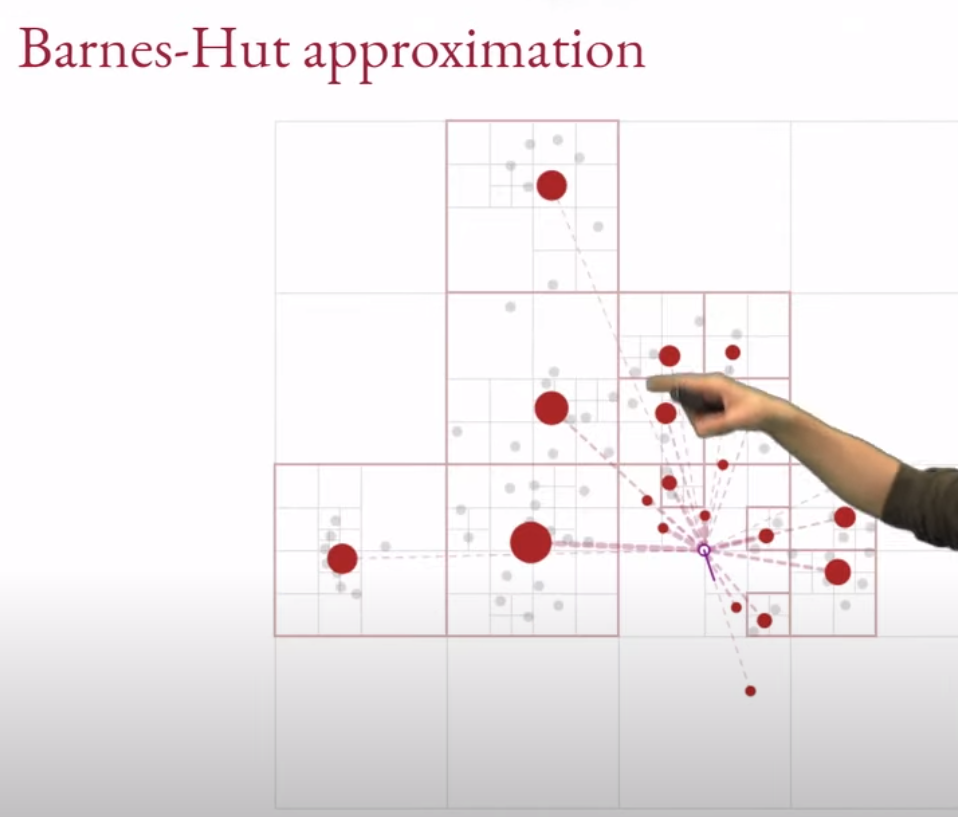
  • We replace a grid of points by its representative point

  • Using approximate repulsive forces

  • Barnes-Hut t-SNE O(nlog(n))

  • FFT-accelerated interpolation based t-SNE - O(n)

  • Noise contrastive estimation / negative sampling - O(n)

Hyperparameters of t-SNE

Perplexity

  • Perplexity is the ‘effective’ number of neighbors considered for similarity. Default is 30

  • t-SNE with different perplexities

  • Much smaller values of perplexity is not useful

  • Much larger values are computationally prohibitive

Kernal

  • Kernel - Heavy tailed kernel provide more fain grained cluster results
  • t-SNE uses Cauchy kernel (distribution with heavier tails)

Role of initialization

  • t-SNE preserves local structure (neighbours) but often struggle to preserve global structure. The loss function has many local minima and intialization can play a large role
  • We can use PCA as initialization for t-SNE

Exaggeration

  • Attraction-repulsion spectrum

  • If the Exaggeration is very high then the white space between clusters is reduced

  • If the Exaggeration is not there then the points in a cluster will end up in different places due to repulsion

Reference