Stats Revisited

  • With standard error, we can create an interval that will contain the true mean 95% of the time (error is for estimating true mean from the mean of the means of experiment).

  • Confidence interval is calculated when we don’t have the luxury of simulating the same experiment with multiple datasets.To calculate confidence interval, we use the central limit theorem.As 95% of the mass of normal distribution is between 1.96 (close to 2) standard errors, we multiply standard error by 2 and add and subtract it from the mean of one of our experiments, we will construct a 95% confidence interval for the true mean. (In practice we multiple by Z which is a cumulative density function instead of 2). If sample size is small, the larger the standard error and wider the confidence interval.

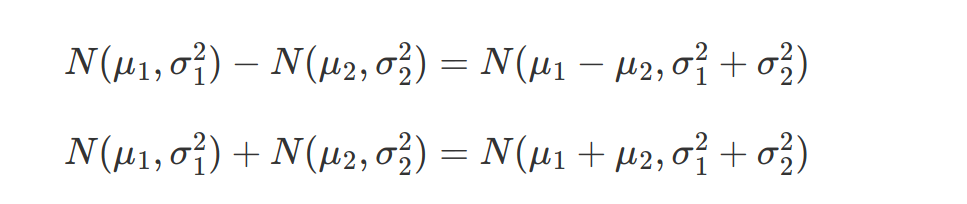
  • The sum or difference of 2 independent normal distributions is also normal distribution. The resulting mean will be the sum or difference between the two distributions, while the variance will always be the sum of the variance. Sum of Normal distribution

  • P-values - It measures how unlikely is the measurement given that null hypothesis is true. p-values is P(data|Null Hypothesis is True) p-value

Code to do AB Testing in python

def AB_test(test: pd.Series, control: pd.Series, confidence=0.95, h0=0):
    mu1, mu2 = test.mean(), control.mean()
    se1, se2 = test.std() / np.sqrt(len(test)), control.std() / np.sqrt(len(control))
    
    diff = mu1 - mu2
    se_diff = np.sqrt(test.var()/len(test) + control.var()/len(control))
    
    z_stats = (diff-h0)/se_diff
    p_value = stats.norm.cdf(z_stats)
    
    def critial(se): return -se*stats.norm.ppf((1 - confidence)/2)
    
    print(f"Test {confidence*100}% CI: {mu1} +- {critial(se1)}")
    print(f"Control {confidence*100}% CI: {mu2} +- {critial(se2)}")
    print(f"Test-Control {confidence*100}% CI: {diff} +- {critial(se_diff)}")
    print(f"Z Statistic {z_stats}")
    print(f"P-Value {p_value}")