Determinants

Singular and Non-Singular Transformations

  • Linear transformations which are non-singular will cover the entire plane

  • Linear transformations which are Singular will not cover the whole plane

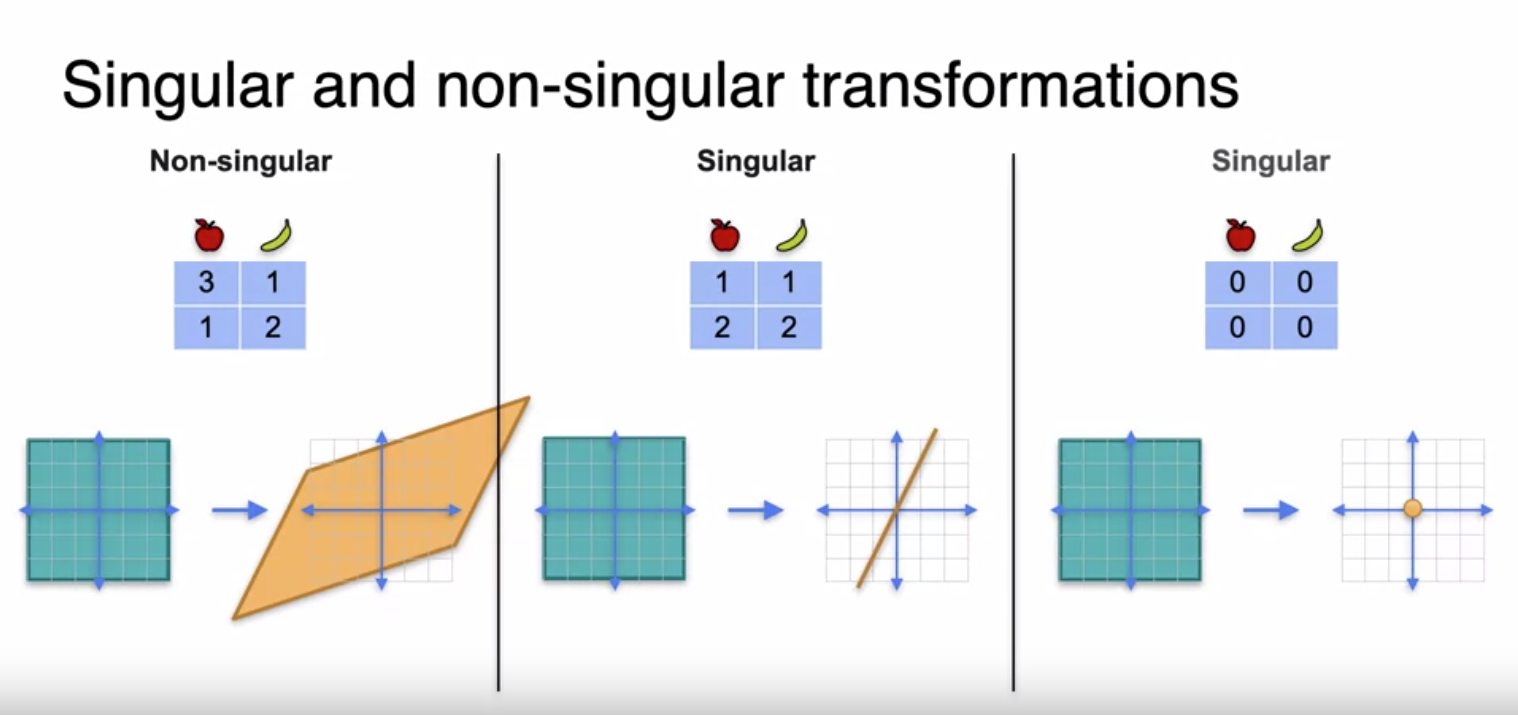
  • Singular and Non-Singular Transformations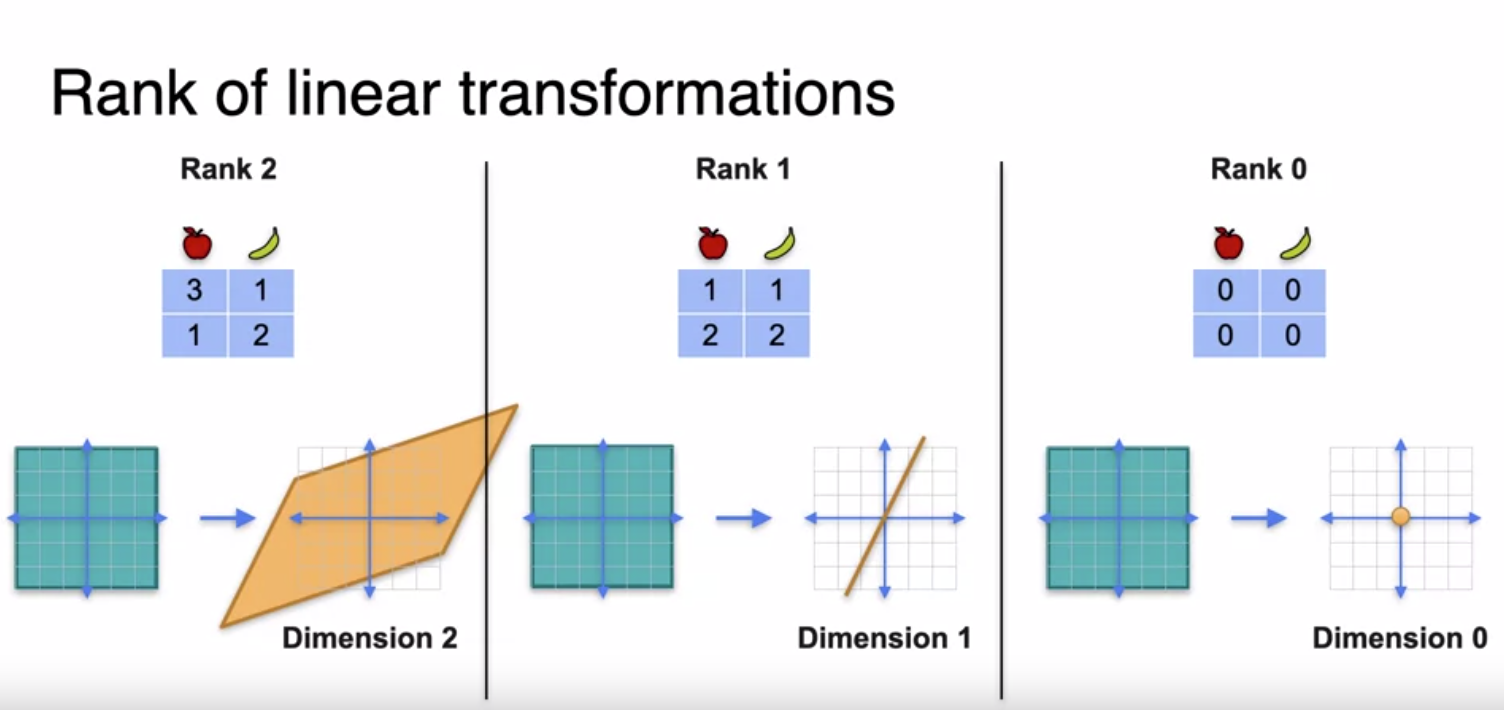

  • Rank and dimension of linear transform

Determinant as an area

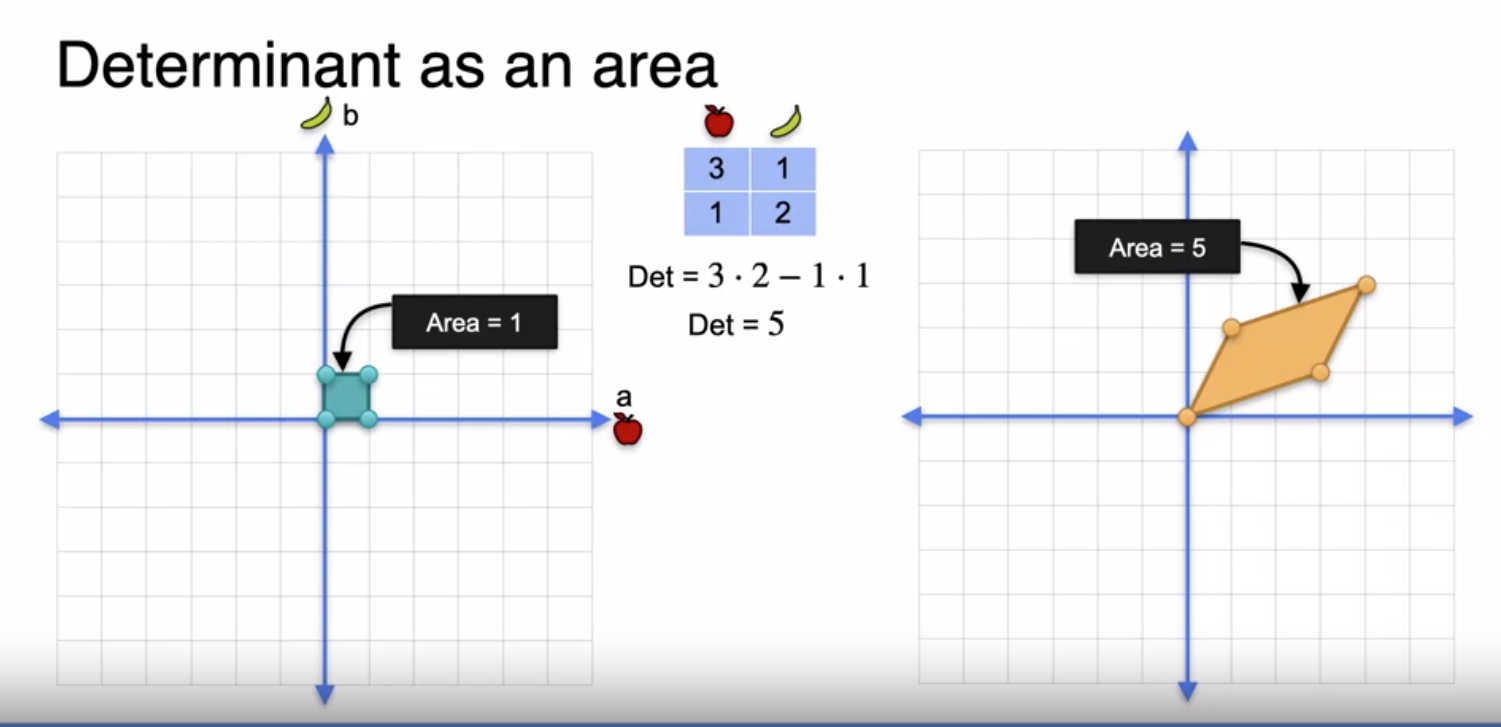
  • Determinant as an area

  • For singular matrix the area of determinant is zero

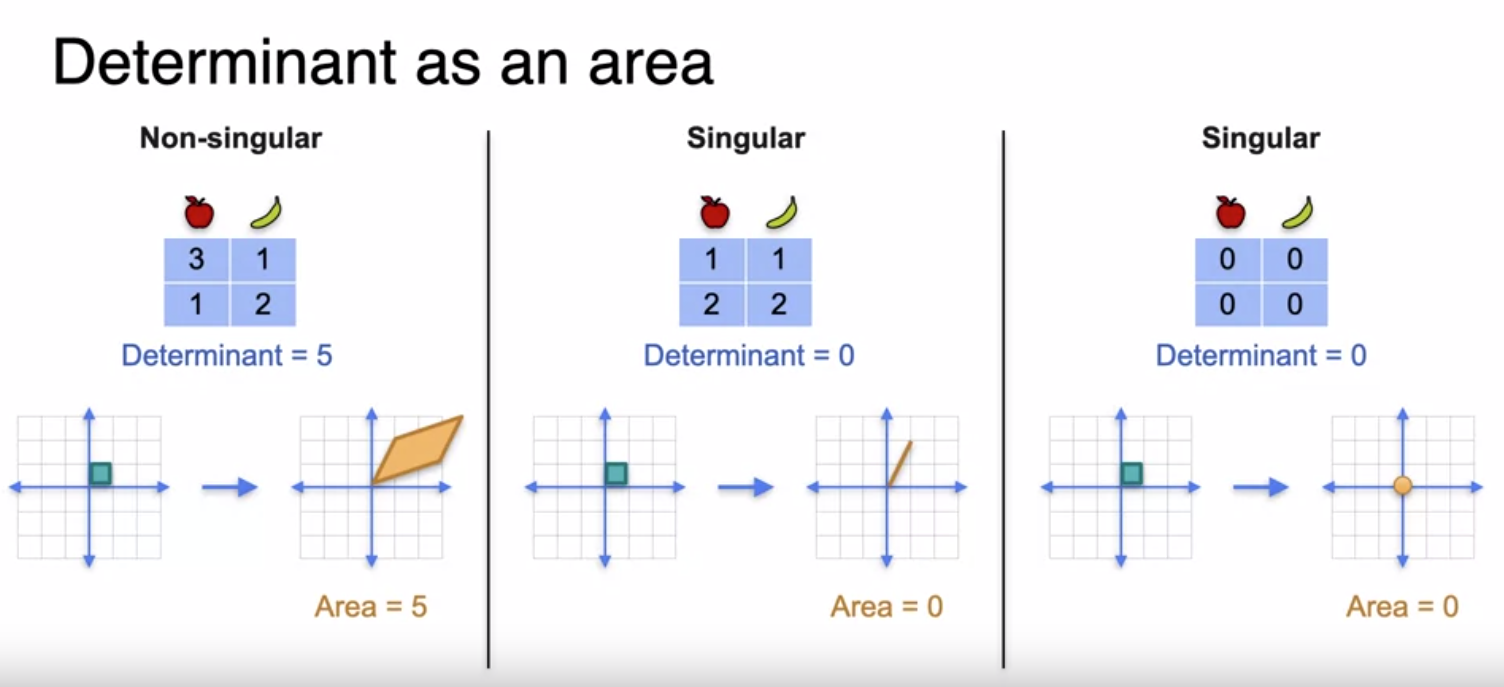
  • Determinant of singular and non-singular matrix

Determinant of a Product

  • det(AB) = det(A)*det(B)

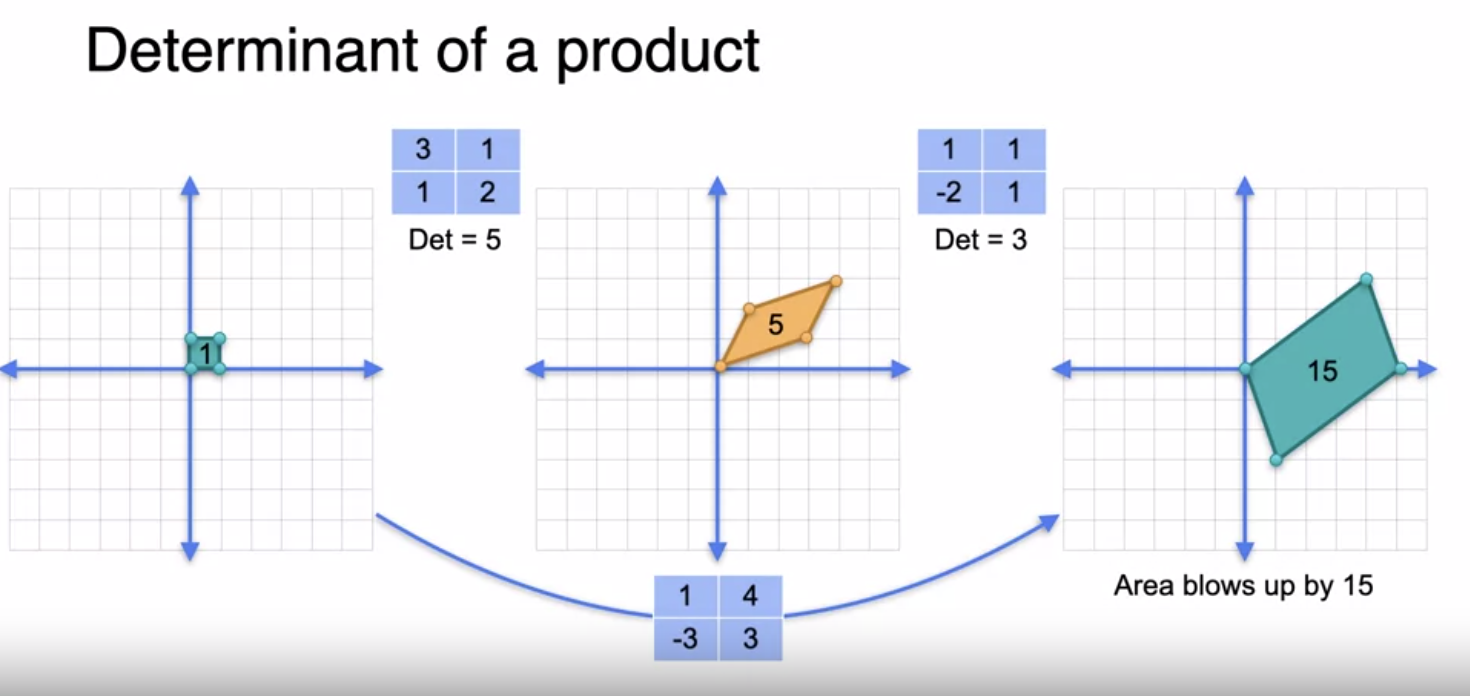
  • Determinant of a product

  • The determinant of a product of singular and non-singular is zero, so AB will be singular

Determinants of Inverses

  • The determinant of an inverse matrix is the inverse of the determinant of the matrix
  • Determinant of an inverse matrix