System of Linear Equations

  • A system can be either singular or non-singular
  • If the system is redundant or contradictory then it is singular
  • IF the system carries as many pieces of information as sentences then it is a complete system, which is called non-singular
  • We can measure how redundant a system is using Rank
  • System of Sentences

Singular and non-singular equations

  • If the system does not carry enough information then it can have infinite solutions

  • System without enough information

  • System with contradictory information

  • Singular and non-singular systems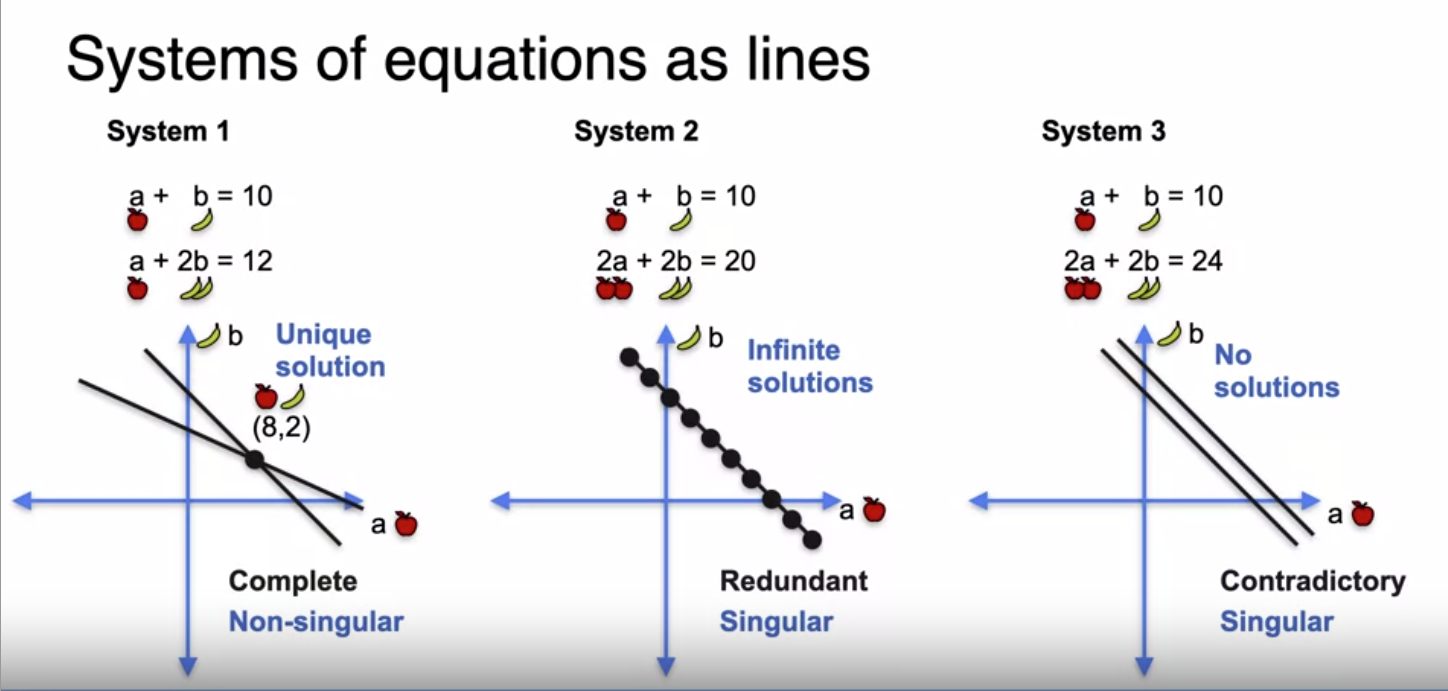

  • System of Equations as lines

  • The constants does not matter when it comes to determine if the system is singular or non-singular. We can consider the constants as zero to make the equations simpler

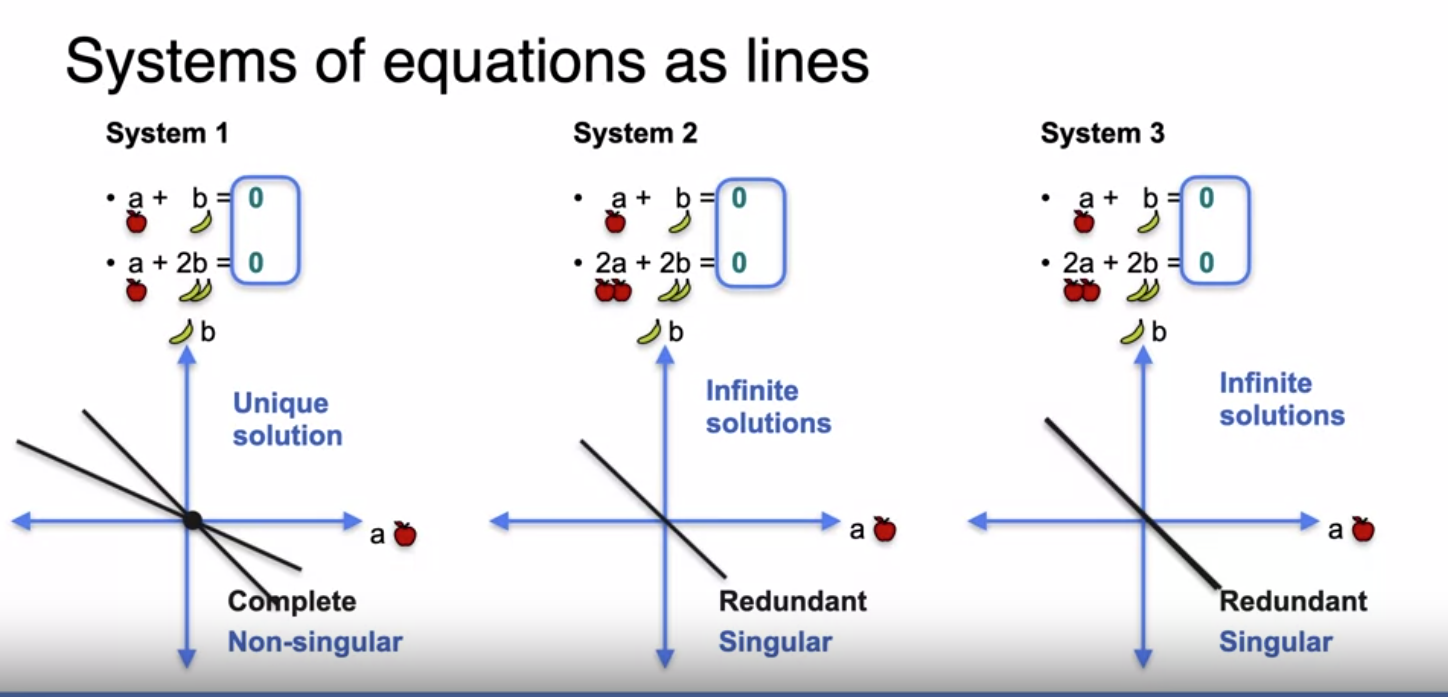
  • Lines with Zero constants which goes through the origin

Linear dependence and independence

  • If a row can be obtained from another row, then the second row is dependent on the first one. They are linearly dependent. Otherwise it is independent. The same applies for columns in a matrix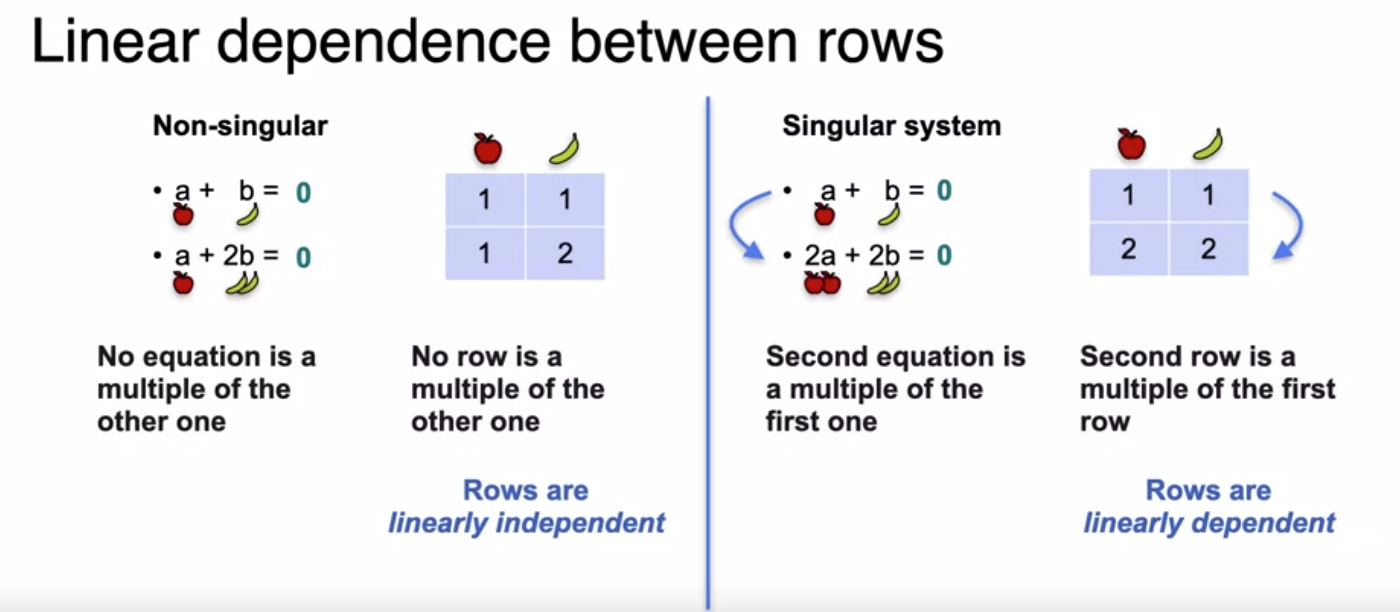
  • Linear and non-linear dependency

Determinant

  • If the determinant is zero then the matrix is singular. Otherwise the matrix is non-singular

  • Caculating Determinant

  • For matrices bigger than 2x2, calculating the determinant is more involved. We need to wrap around and consider all the diagonals. See the picture below for 3x3 matrix

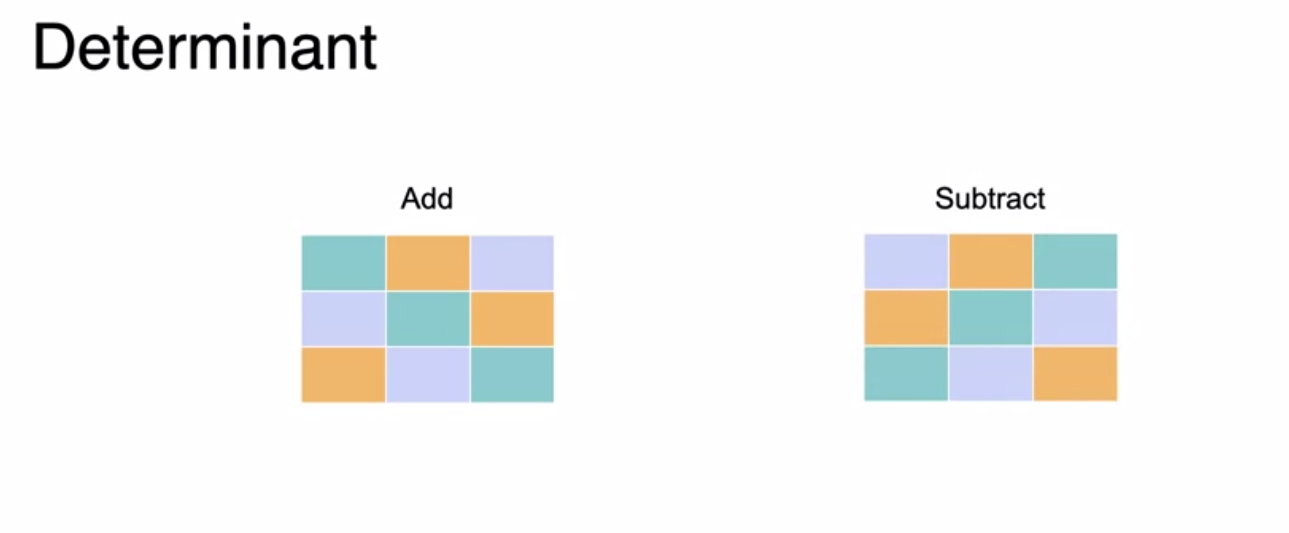
  • Caclulating the determinant for 3x3 matrix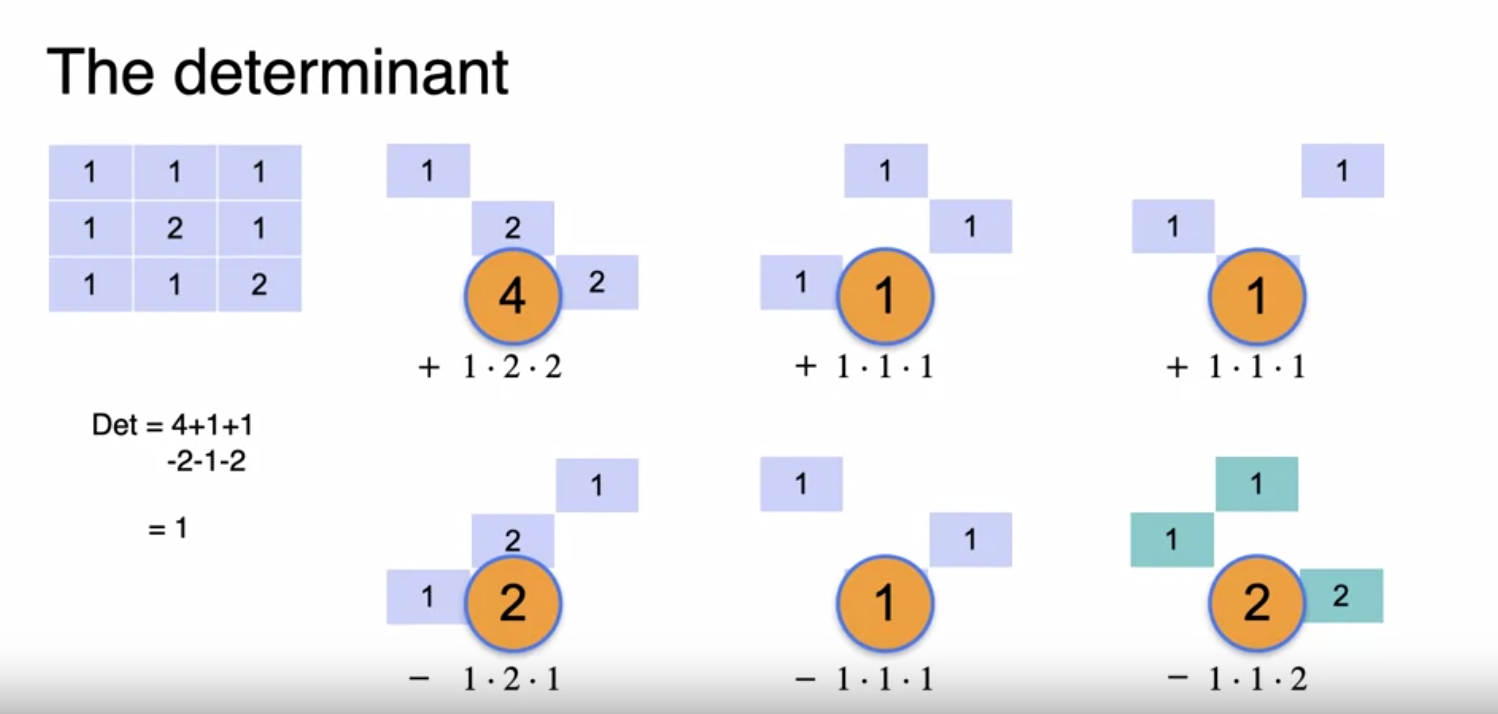

  • Steps in calculating the determinant

  • Upper Traingular Matrix is a matrix in which all the values below the diagonal is zero. For such a matrix, the determinant is the product of main diagonal because all other multiplication operations will have zero in it. (see the figure below)

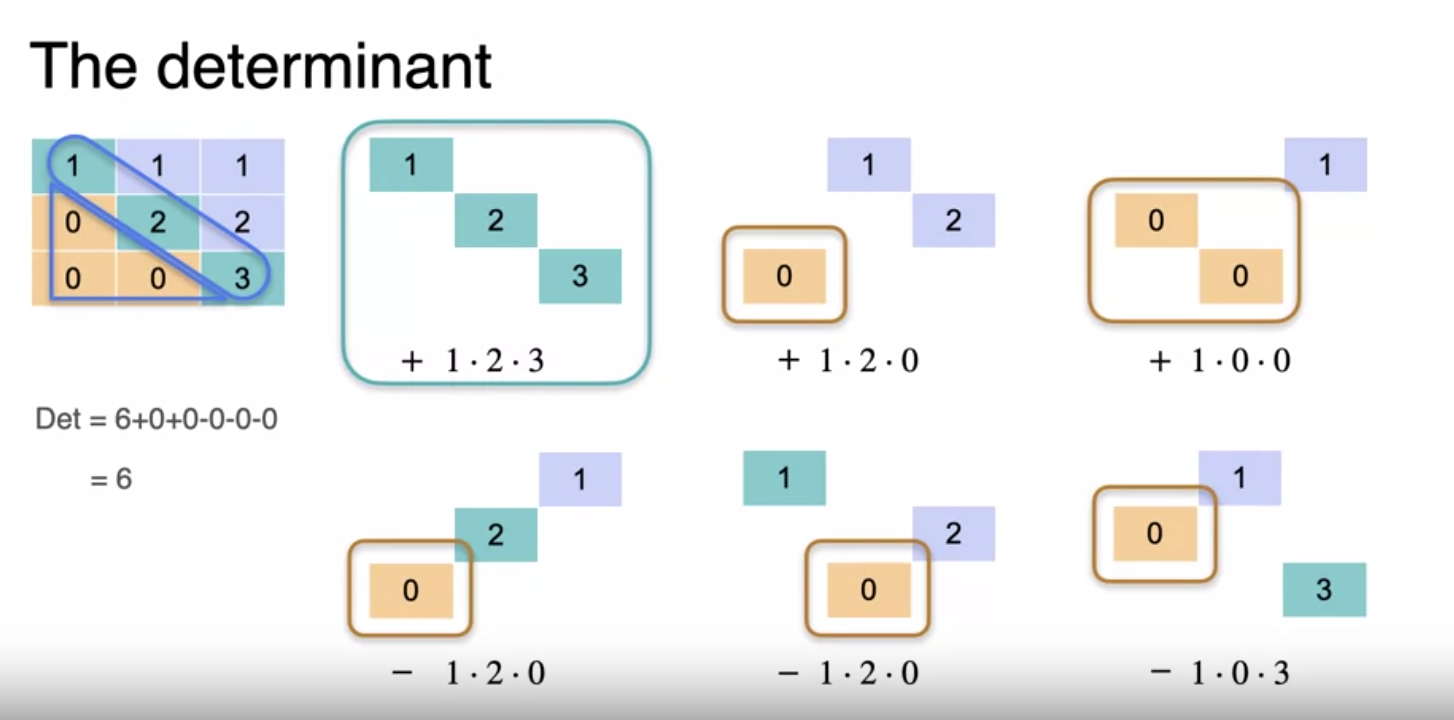
  • Determinant for upper traingle matrix

Reference